题目内容
2.已知下列命题:①若a≤0,则|a|=一a;②当a>b时,若c>0,则ac>bc;
③直角三角形斜边上的中线等于斜边的一半;④矩形的两条对角线相等
其中原命题与逆命题均为真命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据绝对值的意义对①进行判断;根据不等式的性质对②进行判断;根据直角三角形斜边上的中线性质对③进行判断;根据矩形的性质对④进行判断.
解答 解:若a≤0,则|a|=-a,所以①正确;
当a>b时,若c>0,则ac>bc,所以②正确;
直角三角形斜边上的中线等于斜边的一半,所以③正确;
矩形的两条对角线相等,所以④正确.
故选D.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.

练习册系列答案
相关题目
13.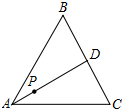 如图,P为等边△ABC的中线AD上一点,AD=3AP,在边AB、AC上分别取点M、N,使△PMN为以MN为底的等腰直角三角形,若AP=1+$\sqrt{3}$,则MN的长为( )
如图,P为等边△ABC的中线AD上一点,AD=3AP,在边AB、AC上分别取点M、N,使△PMN为以MN为底的等腰直角三角形,若AP=1+$\sqrt{3}$,则MN的长为( )
 如图,P为等边△ABC的中线AD上一点,AD=3AP,在边AB、AC上分别取点M、N,使△PMN为以MN为底的等腰直角三角形,若AP=1+$\sqrt{3}$,则MN的长为( )
如图,P为等边△ABC的中线AD上一点,AD=3AP,在边AB、AC上分别取点M、N,使△PMN为以MN为底的等腰直角三角形,若AP=1+$\sqrt{3}$,则MN的长为( )| A. | 2 | B. | 4+2$\sqrt{3}$ | C. | 2$\sqrt{2}$+$\sqrt{6}$ | D. | 4+2$\sqrt{3}$或2 |
10.重庆市奉节县以盛产脐橙而闻名,春节期间,达州市一水果批发经销商为满足市场需要,安排15辆汽车到奉节县装运A、B、C三种不同品质的脐橙120吨到达州销售,按计划15辆汽车都要装满县每辆汽车只能装同一种品质的脐橙,每种脐橙所用车辆都不少于3辆.
(1)设装运A种脐橙的车辆数为x辆,装运B种脐橙车辆数为y辆,根据下表提供的信息,求出y与x之间的函数关系式;
(2)在(1)条件下,求出该函数自变量x的取值范围,车辆的安排方案共有几种?请写出每种安排方案;
(3)为了减少脐橙积压,奉节县政府制定出台了促进脐橙销售的优惠政策,在外地运销客户原有获利不变的情况下,政府对外地运销商按每吨60元的标准实行运费补贴.若外地运销商要想所获利润W(元)最大,应采用哪种车辆安排方案?并求出利润W(元)的最大值?
(1)设装运A种脐橙的车辆数为x辆,装运B种脐橙车辆数为y辆,根据下表提供的信息,求出y与x之间的函数关系式;
| 脐橙品种 | A | B | C |
| 每辆汽车运载(吨) | 10 | 8 | 6 |
| 每吨脐橙所获利润(元) | 600 | 1000 | 800 |
(3)为了减少脐橙积压,奉节县政府制定出台了促进脐橙销售的优惠政策,在外地运销客户原有获利不变的情况下,政府对外地运销商按每吨60元的标准实行运费补贴.若外地运销商要想所获利润W(元)最大,应采用哪种车辆安排方案?并求出利润W(元)的最大值?
17. 如图所示,已知AC∥ED,∠C=30°,∠CBE=40°,则∠BED的度数是( )
如图所示,已知AC∥ED,∠C=30°,∠CBE=40°,则∠BED的度数是( )
 如图所示,已知AC∥ED,∠C=30°,∠CBE=40°,则∠BED的度数是( )
如图所示,已知AC∥ED,∠C=30°,∠CBE=40°,则∠BED的度数是( )| A. | 60° | B. | 80° | C. | 70° | D. | 50° |
7.在四张完全相同的卡片上,分别画有平行四边形、菱形、等腰三角形、等腰梯形,现从中随机抽取一张,卡片上的图形恰好是中心对称图形的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
14.设计一张折叠型方桌子如图,若AO=BO=50cm,CO=DO=30cm,将桌子放平后,要使AB距离地面的高为40cm,则两条桌腿需要叉开的∠AOB应为( )
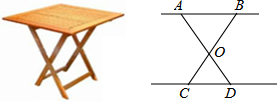

| A. | 60° | B. | 90° | C. | 120° | D. | 150° |