题目内容
14.设计一张折叠型方桌子如图,若AO=BO=50cm,CO=DO=30cm,将桌子放平后,要使AB距离地面的高为40cm,则两条桌腿需要叉开的∠AOB应为( )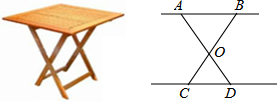
| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
分析 作DE⊥AB于E,根据题意,得在Rt△ADE中,AD=50+30=80cm,DE=40cm,由此可以推出∠A=30°,接着可以求出∠B=∠A=30°,再根据三角形的内角和即可求出∠AOB的度数.
解答  解:作DE⊥AB于E.
解:作DE⊥AB于E.
∵AD=50+30=80cm,DE=40cm,
∴∠A=30°,
∵AO=BO,
∴∠B=∠A=30°,
∴∠AOB=180°-30°-30°=120°.
故选C.
点评 此题考查了含30度角的直角三角形的性质,等腰三角形的性质,三角形内角和定理.作出辅助线得到∠A=30°是解题的关键.

练习册系列答案
相关题目
5.观察下列图形的构成规律,按此规律,第20个图形中棋子的个数是( )


| A. | 114 | B. | 214 | C. | 424 | D. | 444 |
2.已知下列命题:
①若a≤0,则|a|=一a;②当a>b时,若c>0,则ac>bc;
③直角三角形斜边上的中线等于斜边的一半;④矩形的两条对角线相等
其中原命题与逆命题均为真命题的个数是( )
①若a≤0,则|a|=一a;②当a>b时,若c>0,则ac>bc;
③直角三角形斜边上的中线等于斜边的一半;④矩形的两条对角线相等
其中原命题与逆命题均为真命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.二次函数y=x2-|k|与正比例函数y=kx(k≠0)图象的位置关系为( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 不能确定 |
3.下列四个数中,最小的数是( )
| A. | 0 | B. | 1 | C. | -$\frac{1}{2}$ | D. | -1 |
 如图,抛物线y=-$\frac{1}{2}$x2+4x-6与x轴相交于点A,B,与y轴相交于点C,抛物线的对称轴与x轴相交于点M.
如图,抛物线y=-$\frac{1}{2}$x2+4x-6与x轴相交于点A,B,与y轴相交于点C,抛物线的对称轴与x轴相交于点M.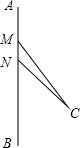 “村村通公路”工程是国家为支持新农村建设的一项重大举措,为了落实这一举措,重庆潼南县政府计划在南北方向的A、B两村之间建一条公路AB.已知公路AB的一侧有C村,在公路AB上的M处测得C村在M的南偏东37°方向上,从M向南走270米到达N处,测得C村在N的东南方向上,且C村周围800米范围内为油菜花田,那么计划修建的公路AB是否会穿过油菜花田,请说明理由(参考数据:sin37°≈0.8,cos37°≈0.8,tan37°≈0.75)
“村村通公路”工程是国家为支持新农村建设的一项重大举措,为了落实这一举措,重庆潼南县政府计划在南北方向的A、B两村之间建一条公路AB.已知公路AB的一侧有C村,在公路AB上的M处测得C村在M的南偏东37°方向上,从M向南走270米到达N处,测得C村在N的东南方向上,且C村周围800米范围内为油菜花田,那么计划修建的公路AB是否会穿过油菜花田,请说明理由(参考数据:sin37°≈0.8,cos37°≈0.8,tan37°≈0.75)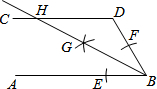 如图,AB∥CD,以点B为圆心,小于DB长为半径作圆弧,分别交BA、BD于点E、F,再分别以点E、F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两弧交于点G,作射线BG交CD于点H.若∠D=116°,则∠DHB的大小为32度.
如图,AB∥CD,以点B为圆心,小于DB长为半径作圆弧,分别交BA、BD于点E、F,再分别以点E、F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两弧交于点G,作射线BG交CD于点H.若∠D=116°,则∠DHB的大小为32度.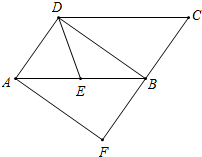 如图,在?ABCD中,E为边AB的中点,BD是对角线,AF∥DB交CB的延长线于F.若DE=BE,则四边形AFBD是什么特殊四边形?并证明你的结论.
如图,在?ABCD中,E为边AB的中点,BD是对角线,AF∥DB交CB的延长线于F.若DE=BE,则四边形AFBD是什么特殊四边形?并证明你的结论.