题目内容
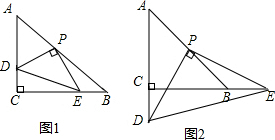
12.在△ABC中,AC=BC,∠C=90°,将一块等腰直角三角尺的直角顶点放在斜边AB的中点P处,绕点P旋转(1)如图1,三角尺的两条直角边分别交边AC,BC于D,E两点,求证:△PDE为等腰三角形.
(2)如图2,三角尺的两条直角边分别交射线AC,射线CB于D,E两点.(1)中的结论还成立吗?请说明理由.
分析 (1)先证明∠BPE=∠PCD,再由ASA证明△PBE≌△PCD,即可得出PE=PD;
(2)同(1),即可得出结论.
解答 (1)证明:连接CP,如图1所示: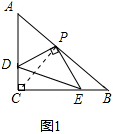
∵AC=BC,∠C=90°,P为斜边的中点,
∴PC⊥AB,PC=$\frac{1}{2}$AB=PB,∠PCD=∠B=45°,
∴∠BPE+∠EPC=90°,∠DPC+∠EPC=90°,
∴∠BPE=∠PCD,
在△PBE和△PCD中,$\left\{\begin{array}{l}{∠B=∠PCD}&{\;}\\{PB=PC}&{\;}\\{∠BPE=∠DPC}&{\;}\end{array}\right.$,
∴△PBE≌△PCD(ASA),
∴PE=PD,
即△PDE为等腰三角形;
(2)结论成立;理由如下:
连接CP,如图所示: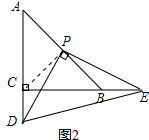
由(1)得:∠BPE=∠PCD,∠PCD=90°+45°=135°,∠PBE=180°-45°=135°,
∴∠PCD=∠PBE,
同(1)可证:△PBE≌△PCD(ASA),
∴PE=PD,
即△PDE为等腰三角形.
点评 本题考查了等腰直角三角形的性质以及全等三角形的判定与性质;证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
2.已知下列命题:
①若a≤0,则|a|=一a;②当a>b时,若c>0,则ac>bc;
③直角三角形斜边上的中线等于斜边的一半;④矩形的两条对角线相等
其中原命题与逆命题均为真命题的个数是( )
①若a≤0,则|a|=一a;②当a>b时,若c>0,则ac>bc;
③直角三角形斜边上的中线等于斜边的一半;④矩形的两条对角线相等
其中原命题与逆命题均为真命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.下列四个数中,最小的数是( )
| A. | 0 | B. | 1 | C. | -$\frac{1}{2}$ | D. | -1 |
7.用48m长的篱笆在空地上围成一个正六边形的绿化场地,那么这个场地的面积为( )
| A. | 16$\sqrt{3}$m2 | B. | 32$\sqrt{3}$m2 | C. | $\sqrt{3}$m2 | D. | 96$\sqrt{3}$m2 |
 已知直线y1=x+b与抛物线y2=-x2+ax+c的一个交点为(2,3),且x=1为该抛物线的对称轴.
已知直线y1=x+b与抛物线y2=-x2+ax+c的一个交点为(2,3),且x=1为该抛物线的对称轴.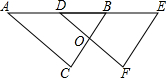 如图,△DEF是由△ABC经过平移得到的,若∠E=70°,∠A=33°,则∠ABC的度数是70°.
如图,△DEF是由△ABC经过平移得到的,若∠E=70°,∠A=33°,则∠ABC的度数是70°.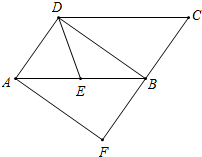 如图,在?ABCD中,E为边AB的中点,BD是对角线,AF∥DB交CB的延长线于F.若DE=BE,则四边形AFBD是什么特殊四边形?并证明你的结论.
如图,在?ABCD中,E为边AB的中点,BD是对角线,AF∥DB交CB的延长线于F.若DE=BE,则四边形AFBD是什么特殊四边形?并证明你的结论.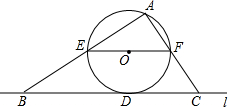 如图,直线L与⊙O相切于点D.过圆心O作EF∥L交⊙O于E、F两点,点A是⊙O上一点,连接AE、AF.并分别延长交直线L于 B、C两点.
如图,直线L与⊙O相切于点D.过圆心O作EF∥L交⊙O于E、F两点,点A是⊙O上一点,连接AE、AF.并分别延长交直线L于 B、C两点.