题目内容
5. 关于x的反比例函数y=$\frac{k}{x}$(k为常数)的图象如图所示,则一次函数y=kx+2-k的图象大致是( )
关于x的反比例函数y=$\frac{k}{x}$(k为常数)的图象如图所示,则一次函数y=kx+2-k的图象大致是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据反比例函数y=$\frac{k}{x}$的图象所在的象限确定k<0.然后根据k<0确定一次函数y=kx+2-k的图象的单调性及与y轴的交点的大体位置,从而确定该一次函数图象所经过的象限.
解答 解:根据图示知,反比例函数y=$\frac{k}{x}$的图象位于第二、四象限,
∴k<0,
∴一次函数y=kx+2-k的图象与y轴的交点在y轴的正半轴,且该一次函数在定义域内是减函数,
∴一次函数y=kx+2-k的图象经过第一、二、四象限;
故选C.
点评 本题考查了反比例函数、一次函数的图象.反比例函数y=$\frac{k}{x}$的图象是双曲线,当k>0时,它的两个分支分别位于第一、三象限;当k<0时,它的两个分支分别位于第二、四象限.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.已知实数m、n,若m<n,则下列结论成立的是( )
| A. | m-3<n-3 | B. | 2+m>2+n | C. | $\frac{m}{2}$>$\frac{n}{2}$ | D. | -3m<-3n |
20. 如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3、4及x,那么x的值( )
如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3、4及x,那么x的值( )
 如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3、4及x,那么x的值( )
如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3、4及x,那么x的值( )| A. | 只有1个 | B. | 可以有2个 | C. | 可以有3个 | D. | 有无数个 |
17.下列各组数中,互为相反数的是( )
| A. | 3和$\frac{1}{3}$ | B. | 3和-3 | C. | 3和-$\frac{1}{3}$ | D. | -3和-$\frac{1}{3}$ |
14.下列说法中错误的是( )
| A. | 0没有平方根 | B. | $\sqrt{5}$是无理数 | ||
| C. | 任何实数都有立方根 | D. | 9的平方根是±3 |
15.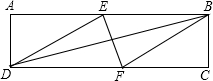 如图,在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB、CD上),记它们的面积分别为SABCD和SBFDE.现给出下列命题:
如图,在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB、CD上),记它们的面积分别为SABCD和SBFDE.现给出下列命题:
①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,则tan∠EDF=$\frac{\sqrt{3}}{3}$;
②若DE2=BD•EF,则DF=2AD.
那么,下面判断正确的是( )
 如图,在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB、CD上),记它们的面积分别为SABCD和SBFDE.现给出下列命题:
如图,在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB、CD上),记它们的面积分别为SABCD和SBFDE.现给出下列命题:①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,则tan∠EDF=$\frac{\sqrt{3}}{3}$;
②若DE2=BD•EF,则DF=2AD.
那么,下面判断正确的是( )
| A. | ①是真命题,②是真命题 | B. | ①是真命题,②是假命题 | ||
| C. | ①是假命题,②是真命题 | D. | ①假命题,②假命题 |
 如图,在平行四边形ABCD中,AB=8,AD=6,∠DAB=30°,E、F是对角线AC的三等分点,则△BEF的面积是4.
如图,在平行四边形ABCD中,AB=8,AD=6,∠DAB=30°,E、F是对角线AC的三等分点,则△BEF的面积是4.