题目内容
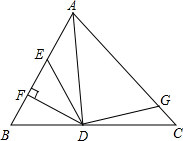如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为50和38，则△EDF的面积为（ ）| A、8 | B、12 | C、4 | D、6 |
考点：角平分线的性质
专题：
分析：过点D作DH⊥AC于H，根据角平分线上的点到角的两边距离相等可得DF=DH，然后利用“HL”证明Rt△DEF和Rt△DGH全等，根据全等三角形的面积相等可得S△EDF=S△GDH，设面积为S，然后根据S△ADF=S△ADH列出方程求解即可．
解答：
解：如图，过点D作DH⊥AC于H，
∵AD是△ABC的角平分线，DF⊥AB，
∴DF=DH，
在Rt△DEF和Rt△DGH中，
，
∴Rt△DEF≌Rt△DGH（HL），
∴S△EDF=S△GDH，设面积为S，
同理Rt△ADF≌Rt△ADH，
∴S△ADF=S△ADH，
即38+S=50-S，
解得S=6．
故选D．
解：如图，过点D作DH⊥AC于H，∵AD是△ABC的角平分线，DF⊥AB，
∴DF=DH，
在Rt△DEF和Rt△DGH中，
|
∴Rt△DEF≌Rt△DGH（HL），
∴S△EDF=S△GDH，设面积为S，
同理Rt△ADF≌Rt△ADH，
∴S△ADF=S△ADH，
即38+S=50-S，
解得S=6．
故选D．
点评：本题考查了角平分线上的点到角的两边距离相等的性质，全等三角形的判定与性质，作辅助线构造出全等三角形并利用角平分线的性质是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
若2m2n2•B=14m4n3-8m3n3，那么B=（ ）
| A、7mn2-4mn |
| B、28m2n-16n |
| C、7m2n-4mn |
| D、7m2-4n |
如图，菱形花坛ABCD的边长为20m，∠ABC=60°，沿着该菱形的对角线修建两条小路AC和BD，花坛的面积