题目内容
19. 如图,∠AOB=35°,P是∠AOB内任意一点,P1、P2分别是点P关于OA、OB的对称点,连接P1P2与OA、OB分别交于点C、D,若P1P2=16cm,则△PCD的周长是16cm,∠P1OP2=70°.
如图,∠AOB=35°,P是∠AOB内任意一点,P1、P2分别是点P关于OA、OB的对称点,连接P1P2与OA、OB分别交于点C、D,若P1P2=16cm,则△PCD的周长是16cm,∠P1OP2=70°.
分析 首先根据点P关于OA、OB的对称点分别是P1,P2,可得PD=P1D,PC=P2C;然后根据P1P2=16cm,可得P1D+DC+P2C=16cm,所以PD+DC+PC=16cm,即△PCD的周长为16cm,据此解答即可.
解答 解:∵点P关于OA、OB的对称点分别是P1,P2,
∴PD=P2D,PC=P1C;
∵P1P2=16(cm),
∴P1D+DC+P2C=16(cm),
∴PD+DC+PC=16(cm),
即△PCD的周长为16cm.
∠P1OP2=2∠AOB=2×35°=70°,
故答案为:16cm,70°.
点评 (1)此题主要考查了轴对称的性质的应用,要熟练掌握,解答此题的关键是判断出:PD=P1D,PC=P2C.
(2)此题还考查了三角形的周长的含义以及求法的应用,要熟练掌握.

练习册系列答案
相关题目
4. 正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2015次后,数轴上数2015所对应的点是( )
正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2015次后,数轴上数2015所对应的点是( )
 正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2015次后,数轴上数2015所对应的点是( )
正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2015次后,数轴上数2015所对应的点是( )| A. | 点C | B. | 点D | C. | 点A | D. | 点B |
11.下列实数中,是无理数的为( )
| A. | 0.3 | B. | 0 | C. | $\sqrt{3}$ | D. | $\frac{1}{3}$ |
9.抛物线y=(x+1)(x-3)的对称轴是直线( )
| A. | x=-1 | B. | x=1 | C. | x=-3 | D. | x=3 |

 如图,正方体的六个面上标着六个连续的整数,若相对的两个面上所标之数的和相等,则这6个数的和为75或81.
如图,正方体的六个面上标着六个连续的整数,若相对的两个面上所标之数的和相等,则这6个数的和为75或81.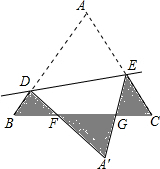 如图,等边△ABC的面积为为$\sqrt{3}$cm2,D、E分别是AB、AC上的点,将△ABC沿直线DE折叠,点A落在A′处,且A′在△ABC外部,则阴影部分图象的周长为6cm.
如图,等边△ABC的面积为为$\sqrt{3}$cm2,D、E分别是AB、AC上的点,将△ABC沿直线DE折叠,点A落在A′处,且A′在△ABC外部,则阴影部分图象的周长为6cm.