题目内容
 如图:为了把半径都是30cm的三根圆柱紧紧地捆在一起,绕它们的横截面捆一圈需要多长的铅线(π=3.1,精确到1cm不计捆扎打结部分)?
如图:为了把半径都是30cm的三根圆柱紧紧地捆在一起,绕它们的横截面捆一圈需要多长的铅线(π=3.1,精确到1cm不计捆扎打结部分)?考点:相切两圆的性质
专题:
分析:如图,根据题意可以知道所求的铅线长度为3(AB+
),而
的度数为120°,接着利用弧长公式和相切两圆的性质即可求解.
 |
| AF |
 |
| AF |
解答: 解:如图,∵被铅线捆绑在一起的三根底面半径为30cm的圆两两相切,
解:如图,∵被铅线捆绑在一起的三根底面半径为30cm的圆两两相切,
∴所求铅线长度为3(AB+
),且
的度数为120°,
而AB=30+30=60(cm),l
=
=20π≈63(cm),
∴所求铅线的长度189cm.
答:绕它们的横截面捆一圈需要189的铅线.
 解:如图,∵被铅线捆绑在一起的三根底面半径为30cm的圆两两相切,
解:如图,∵被铅线捆绑在一起的三根底面半径为30cm的圆两两相切,∴所求铅线长度为3(AB+
 |
| AF |
 |
| AF |
而AB=30+30=60(cm),l
 |
| AF |
| 120π×30 |
| 180 |
∴所求铅线的长度189cm.
答:绕它们的横截面捆一圈需要189的铅线.
点评:此题主要考查了相切两圆的性质,解题时首先正确理解题意,然后根据题意得到所求的铅线长度,最后利用弧长公式和相切两圆的性质即可求解.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
世界杯足球赛正在巴西如火如荼地进行,赛前有人预测,巴西国家队夺冠的概率是90%.对他的说法理解正确的是( )
| A、巴西队一定会夺冠 |
| B、巴西队一定不会夺冠 |
| C、巴西队夺冠的可能性很大 |
| D、巴西队夺冠的可能性很小 |
 如图,点P1、P2、P3分别是双曲线同一支图象上的三点,过这三点分别作y轴的垂线,垂足分别是A1、A1、A3,得到的三个三角形△P1A1O、△P2A2O、△P3A3O.设它们的面积分别为S1、S2、S3,则它们的大小关系是( )
如图,点P1、P2、P3分别是双曲线同一支图象上的三点,过这三点分别作y轴的垂线,垂足分别是A1、A1、A3,得到的三个三角形△P1A1O、△P2A2O、△P3A3O.设它们的面积分别为S1、S2、S3,则它们的大小关系是( )| A、S1>S2>S3 |
| B、S3>S2>S1 |
| C、S1=S2=S3 |
| D、S2>S3>S1 |
若反比例函数y=
(k≠0)的图象过点(2,1),则这个函数的图象一定过点( )
| k |
| x |
| A、(2,-1) |
| B、(1,-2) |
| C、(-2,1) |
| D、(-2,-1) |
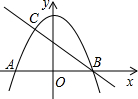 如图,抛物线y=-
如图,抛物线y=-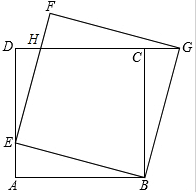 如图,正方形ABCD的边长为1,点E是AD边上的动点,从点A沿AD向D运动,以BE为边,在BE的上方作正方形BEFG,连接CG.
如图,正方形ABCD的边长为1,点E是AD边上的动点,从点A沿AD向D运动,以BE为边,在BE的上方作正方形BEFG,连接CG.