题目内容
先化简,再求值:
÷(x+
)•(
+
),其中x=2+
,y=2-
.
| y2-x2 |
| x2-xy |
| 2xy+y2 |
| x |
| 1 |
| x |
| 1 |
| y |
| 3 |
| 3 |
考点:分式的化简求值
专题:
分析:根据分式的运算法则先化简原式,然后将x和y的值代入化简后的式子求值即可.
解答:解:
÷(x+
)•(
+
)
=
÷
•
=
•
•
=-
,
当x=2+
,y=2-
时,
原式=-
=-1.
| y2-x2 |
| x2-xy |
| 2xy+y2 |
| x |
| 1 |
| x |
| 1 |
| y |
=
| (y+x)(y-x) |
| x(x-y) |
| x2+2xy+y2 |
| x |
| y+x |
| xy |
=
| (y+x)(y-x) |
| x(x-y) |
| x |
| (x+y)2 |
| y+x |
| xy |
=-
| 1 |
| xy |
当x=2+
| 3 |
| 3 |
原式=-
| 1 | ||||
(2+
|
点评:此题考查分式的化简求值,解答此题的关键是把分式化到最简,然后代值计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,∠1=∠2,∠3=30°,则∠4等于( )
如图,∠1=∠2,∠3=30°,则∠4等于( )| A、120° | B、130° |
| C、145° | D、150° |
在-
π,-0.01,-3
,4
,
,
,0中,无理数有( )个.
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 | -27 |
|
| A、1个 | B、2个 | C、3个 | D、4个 |
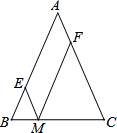 如图,△ABC中,AB=AC=6,点M在BC上,ME∥AC,交AB于点E,MF∥AB,交AC于点F,则四边形MEAF的周长是( )
如图,△ABC中,AB=AC=6,点M在BC上,ME∥AC,交AB于点E,MF∥AB,交AC于点F,则四边形MEAF的周长是( ) 如图:为了把半径都是30cm的三根圆柱紧紧地捆在一起,绕它们的横截面捆一圈需要多长的铅线(π=3.1,精确到1cm不计捆扎打结部分)?
如图:为了把半径都是30cm的三根圆柱紧紧地捆在一起,绕它们的横截面捆一圈需要多长的铅线(π=3.1,精确到1cm不计捆扎打结部分)?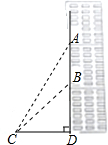 如图,大楼外墙有高为AB的广告牌,由距离大楼20米的点C(即CD=20米)观察它的顶部A的仰角是55°,底部B的仰角是42°,求AB的高度.(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
如图,大楼外墙有高为AB的广告牌,由距离大楼20米的点C(即CD=20米)观察它的顶部A的仰角是55°,底部B的仰角是42°,求AB的高度.(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,sin42°≈0.67,cos42°≈0.74,tan42°≈0.90) 如图一道斜坡AB的坡比为1:10,AC=24米,求斜坡AB的长.
如图一道斜坡AB的坡比为1:10,AC=24米,求斜坡AB的长.