题目内容
 如图,AD⊥DC,AB⊥BC,若AB=AD,∠DAB=120°,则∠ACB的度数为( )
如图,AD⊥DC,AB⊥BC,若AB=AD,∠DAB=120°,则∠ACB的度数为( )| A、60° | B、45° |
| C、30° | D、75° |
考点:角平分线的性质
专题:
分析:根据到角的两边距离相等的点在角的平分线上判断出AC平分∠BCD,再根据四边形的内角和定理求出∠BCD,然后求解即可.
解答:解:∵AD⊥DC,AB⊥BC,AB=AD,
∴AC平分∠BCD,
∵∠DAB=120°,
∴∠BCD=360°-90°×2-120°=60°,
∴∠ACB=
∠BCD=
×60°=30°.
故选C.
∴AC平分∠BCD,
∵∠DAB=120°,
∴∠BCD=360°-90°×2-120°=60°,
∴∠ACB=
| 1 |
| 2 |
| 1 |
| 2 |
故选C.
点评:本题考查了角平分线的性质,熟记到角的两边距离相等的点在角的平分线上是解题的关键.

练习册系列答案
相关题目
下列语句错误的是( )
| A、任何数的绝对值都是非负数 |
| B、有公共端点的两条射线组成的图形叫做角 |
| C、任何数都有倒数 |
| D、经过两点有且只有一条直线 |

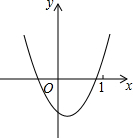 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论①ac<0,②当x>1时,a+b+c>0,③a-b+c>0,其中正确的个数为
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论①ac<0,②当x>1时,a+b+c>0,③a-b+c>0,其中正确的个数为 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=30°,CD=2,则AB的长为
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=30°,CD=2,则AB的长为



 如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,AC=7,AB=8,△ACD的面积是21,则△ABC的面积是
如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,AC=7,AB=8,△ACD的面积是21,则△ABC的面积是