题目内容
如图1,AB是圆O的直径,点C在AB的延长线上,AB=4,BC=2,P是圆O上半部分的一个动点,连接OP,CP.
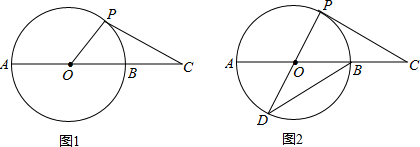
(1)求△OPC的最大面积;
(2)求∠OCP的最大度数;设∠OCP=α,当线段CP与圆O只有一个公共点(即P点)时,求α的范围(直接写出答案);
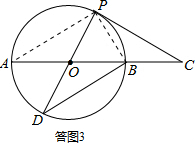
(3)如图2,延长PO交圆O于点D,连接DB,当CP=DB,求证:CP是圆O的切线.
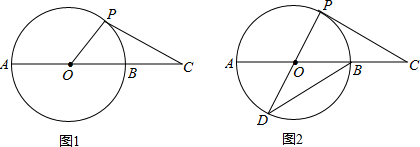
(1)求△OPC的最大面积;
(2)求∠OCP的最大度数;设∠OCP=α,当线段CP与圆O只有一个公共点(即P点)时,求α的范围(直接写出答案);
(3)如图2,延长PO交圆O于点D,连接DB,当CP=DB,求证:CP是圆O的切线.
考点:圆的综合题
专题:
分析:(1)在△OPC中,底边OC长度固定,因此只要OC边上高最大,则△OPC的面积最大;观察图形,当OP⊥OC时满足要求;
(2)PC与⊙O相切时,∠OCP的度数最大,根据切线的性质即可求得.再根据α的最大度数即可得出结论;
(3)连接AP,BP通过△ODB≌△BPC可求得DP⊥PC,从而求得PC是⊙O的切线.
(2)PC与⊙O相切时,∠OCP的度数最大,根据切线的性质即可求得.再根据α的最大度数即可得出结论;
(3)连接AP,BP通过△ODB≌△BPC可求得DP⊥PC,从而求得PC是⊙O的切线.
解答: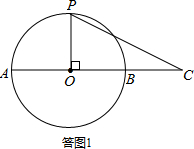 (1)解:∵AB=4,
(1)解:∵AB=4,
∴OB=2,OC=OB+BC=4.
在△OPC中,设OC边上的高为h,
∵S△OPC=
OC•h=2h,
∴当h最大时,S△OPC取得最大值.
观察图形,当OP⊥OC时,h最大,如答图1所示:
此时h=半径=2,S△OPC=2×2=4.
∴△OPC的最大面积为4.
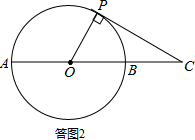
(2)解:当PC与⊙O相切时,∠OCP最大.如答图2所示:
∵sin∠OCP=
=
=
,
∴∠OCP=30°
∴∠OCP的最大度数为30°.
∴设∠OCP=α,当线段CP与圆O只有一个公共点(即P点)时,0<α≤30°;
(3)证明:图3,连接AP,BP.
 ∴∠A=∠D=∠APD=∠ABD,
∴∠A=∠D=∠APD=∠ABD,
∵
=
,
∴
=
,
∴AP=BD,
∵CP=DB,
∴AP=CP,
∴∠A=∠C
∴∠A=∠D=∠APD=∠ABD=∠C,
在△ODB与△BPC中,
,
∴△ODB≌△BPC(SAS),
∴∠D=∠BPC,
∵PD是直径,
∴∠DBP=90°,
∴∠D+∠BPD=90°,
∴∠BPC+∠BPD=90°,
∴DP⊥PC,
∵DP经过圆心,
∴PC是⊙O的切线.
 (1)解:∵AB=4,
(1)解:∵AB=4,∴OB=2,OC=OB+BC=4.
在△OPC中,设OC边上的高为h,
∵S△OPC=
| 1 |
| 2 |
∴当h最大时,S△OPC取得最大值.
观察图形,当OP⊥OC时,h最大,如答图1所示:
此时h=半径=2,S△OPC=2×2=4.
∴△OPC的最大面积为4.

(2)解:当PC与⊙O相切时,∠OCP最大.如答图2所示:
∵sin∠OCP=
| OP |
| OC |
| 2 |
| 4 |
| 1 |
| 2 |
∴∠OCP=30°
∴∠OCP的最大度数为30°.
∴设∠OCP=α,当线段CP与圆O只有一个公共点(即P点)时,0<α≤30°;
(3)证明:图3,连接AP,BP.
 ∴∠A=∠D=∠APD=∠ABD,
∴∠A=∠D=∠APD=∠ABD,∵
 |
| AD |
 |
| PB |
∴
 |
| AP |
 |
| BD |
∴AP=BD,
∵CP=DB,
∴AP=CP,
∴∠A=∠C
∴∠A=∠D=∠APD=∠ABD=∠C,
在△ODB与△BPC中,
|
∴△ODB≌△BPC(SAS),
∴∠D=∠BPC,
∵PD是直径,
∴∠DBP=90°,
∴∠D+∠BPD=90°,
∴∠BPC+∠BPD=90°,
∴DP⊥PC,
∵DP经过圆心,
∴PC是⊙O的切线.
点评:本题考查的是圆的综合题,涉及到全等三角形的判定和性质,切线的判定和性质,作出辅助线构建直角三角形是解题的关键.

练习册系列答案
相关题目
美国NBA职业篮球赛的两支队伍在本赛季已进行了5场比赛,根据统计,两队5场比赛得分的频数分布直方图如下所示,则得分方差较小的队伍是( )


| A、甲 | B、乙 | C、一样大 | D、无法确定 |
若(x+m)(x+n)=x2-6x+5,则( )
| A、m,n同时为负 |
| B、m,n同时为正 |
| C、m,n异号 |
| D、m,n异号且绝对值小的为正 |


 如图,已知:∠A=∠D,∠1=∠2,下列条件中能使△ABC≌△DEF的有
如图,已知:∠A=∠D,∠1=∠2,下列条件中能使△ABC≌△DEF的有 如图,AC⊥DE,垂足为O,∠B=35°,∠E=25°,求∠A的度数.
如图,AC⊥DE,垂足为O,∠B=35°,∠E=25°,求∠A的度数.