��Ŀ����
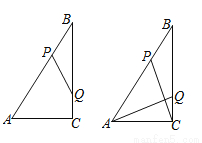
��ͼ��Rt��ABC�У���ACB��90�㣬AC��6cm��BC��8cm������P�ӵ�B��������BA������ÿ��5cm���ٶ����A�����˶���ͬʱ����Q�ӵ�C��������CB������ÿ��4cm���ٶ����B�����˶����˶�ʱ��Ϊt�루0��t��2��������PQ��
��1������BPQ���ABC���ƣ���t��ֵ��
��2����tΪ��ֵʱ���ı���ACQP�������С����Сֵ�Ƕ��٣�
��3������AQ��CP����AQ��CP����t��ֵ��
��ϰ��ϵ�д�
�����Ŀ
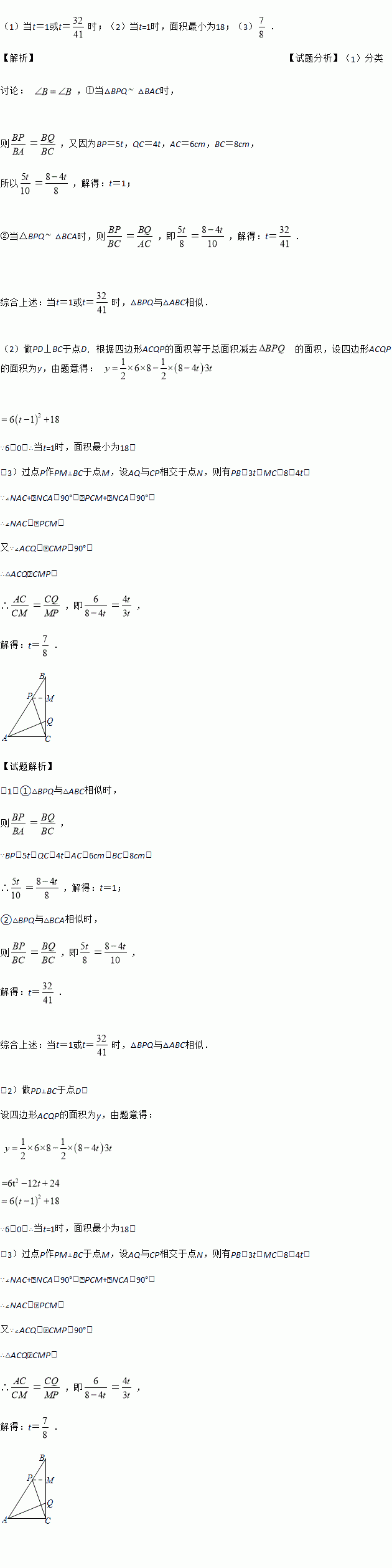

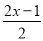 ��
��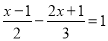 ��ȥ��ĸ��ȷ���ǣ� ��
��ȥ��ĸ��ȷ���ǣ� ��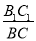 =2���뻭����AB1C1��
=2���뻭����AB1C1��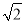 ��
��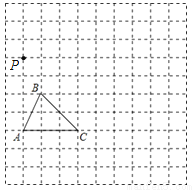
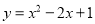 ����Сֵ��________��
����Сֵ��________��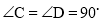 ���������֤�����ɶ�����
���������֤�����ɶ�����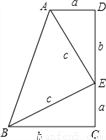
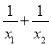 ����_____��
����_____��