题目内容
现有4个一元一次不等式:①x<1;②x<2;③x>4;④x<-1.
(1)从中任取两个不等式,构成的不等式组的解集可能是x>4吗?
(2)从中任取两个不等式,构成的不等式的解集是x<-1的机会有多大?请给予分析并计算概率.
(3)如果用编有号码、大小相同的小球做代替物对题(2)中所得的答案进行验证,请你设计一个模拟的实验方案.
(1)从中任取两个不等式,构成的不等式组的解集可能是x>4吗?
(2)从中任取两个不等式,构成的不等式的解集是x<-1的机会有多大?请给予分析并计算概率.
(3)如果用编有号码、大小相同的小球做代替物对题(2)中所得的答案进行验证,请你设计一个模拟的实验方案.
考点:模拟实验,不等式的解集,列表法与树状图法
专题:
分析:(1)根据不等式组的解集求解方法:大大取大可知构成的不等式组的解集不可能是x>4;
(2)用列表法或画树形图发的到所有可能的情况,即可求出构成的不等式组的解集是x<-1的机会有多大.
(3)设计的模拟实验不唯一,只要事件的概率为
即可.
(2)用列表法或画树形图发的到所有可能的情况,即可求出构成的不等式组的解集是x<-1的机会有多大.
(3)设计的模拟实验不唯一,只要事件的概率为
| 1 |
| 6 |
解答:解:(1)∵4>2>1>-1,
∴从中任取两个不等到式,构成的不等式组的解集不可能是x>4;
(2)列表如下:
所有等可能的情况有12种,其中构成的不等式组的解集是x<-1有2种,所以其概率为
=
;
(3)如:在一个不透明的口袋中,有四个完全相同的小球,把它们分别标号为1、2、3、4,随机地摸取一个小球记下标号后不放回,再随机地摸取一个小球记下标号,则两次摸取的小球标号都是2的概率.
∴从中任取两个不等到式,构成的不等式组的解集不可能是x>4;
(2)列表如下:
| 1 | 2 | 3 | 4 | |
| 1 | (2,1) | (3,1) | (4,1) | |
| 2 | (1,2) | (3,2) | (4,2) | |
| 3 | (1,3) | (2,3) | (4,3) | |
| 4 | (1,4) | (2,4) | (3,4) |
| 2 |
| 12 |
| 1 |
| 6 |
(3)如:在一个不透明的口袋中,有四个完全相同的小球,把它们分别标号为1、2、3、4,随机地摸取一个小球记下标号后不放回,再随机地摸取一个小球记下标号,则两次摸取的小球标号都是2的概率.
点评:本题考查了用列表法与树状图法以及模拟实验,模拟实验是用卡片、小球编号等形式代替实物进行实验,或用计算机编号等进行实验,目的在于省时、省力,但能达到同样的效果.

练习册系列答案
相关题目
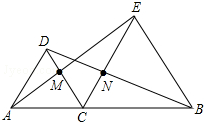 如图,A、C、B三点在同一条直线上,△DAC和△EBC都是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN;④AB=AE.其中,正确结论的个数是( )
如图,A、C、B三点在同一条直线上,△DAC和△EBC都是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN;④AB=AE.其中,正确结论的个数是( )| A、3个 | B、2个 | C、1个 | D、0 |
 如图,AB=AC,EA=ED,∠BAD=20°,∠EDC=10°,则∠B的度数为( )
如图,AB=AC,EA=ED,∠BAD=20°,∠EDC=10°,则∠B的度数为( )| A、45° | B、55° |
| C、50° | D、不能确定 |
点P关于x轴对称点M的坐标为(4,-5),那么点P关于y轴对称点N的坐标为( )
| A、(-4,5) |
| B、(4,-5) |
| C、(-4,-5) |
| D、(-5,-4) |
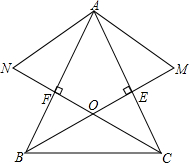 在△ABC中,BE、CF分别是AC、AB边上的高,在BE的延长线上取BM=AC,
在△ABC中,BE、CF分别是AC、AB边上的高,在BE的延长线上取BM=AC,