题目内容
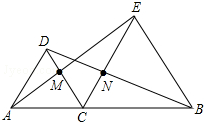如图，A、C、B三点在同一条直线上，△DAC和△EBC都是等边三角形，AE、BD分别与CD、CE交于点M、N，有如下结论：①△ACE≌△DCB；②CM=CN；③AC=DN；④AB=AE．其中，正确结论的个数是（ ）| A、3个 | B、2个 | C、1个 | D、0 |
考点：全等三角形的判定与性质,等边三角形的判定与性质
专题：计算题
分析：由△DAC和△EBC都是等边三角形，利用等边三角形的性质得到AC=CD，EC=BC，且∠ACD=∠ECB=60°，利用等式的性质得到夹角相等，利用SAS得到△ACE≌△DCB，利用全等三角形的对应角相等得到∠AEC=∠DBC，利用平角的定义得到∠DCE=60°，即∠DCE=∠NCB，再由夹边EC=BC，利用ASA得到△EMC≌△BNC，利用全等三角形对应边相等得到CM=CN，即可得到结果．
解答：解：∵△ACD和△ECB都为等边三角形，
∴∠ACD=∠ECB=60°，AC=CD，EC=BC，
∴∠ACD+∠DCE=∠ECB+∠DCE，即∠ACE=∠DCB，
在△ACE和△DCB中，
，
∴△ACE≌△DCB（SAS），
∴∠AEC=∠DBC，
∵∠ACD=∠ECB=60°，
∴∠DCE=60°，
∴∠MCE=∠NCB=60°，
在△MCE和△NCB中，
，
∴△MCE≌△NCB（ASA），
∴CM=CN，
则正确结论个数为2个．
故选B．
∴∠ACD=∠ECB=60°，AC=CD，EC=BC，
∴∠ACD+∠DCE=∠ECB+∠DCE，即∠ACE=∠DCB，
在△ACE和△DCB中，
|
∴△ACE≌△DCB（SAS），
∴∠AEC=∠DBC，
∵∠ACD=∠ECB=60°，
∴∠DCE=60°，
∴∠MCE=∠NCB=60°，
在△MCE和△NCB中，
|
∴△MCE≌△NCB（ASA），
∴CM=CN，
则正确结论个数为2个．
故选B．
点评：此题考查了全等三角形的判定与性质，等边三角形的性质，熟练掌握全等三角形的判定与性质是解本题的关键．
练习册系列答案
相关题目
如图是七年级某班的数学成绩统计图，该班总人数是
如图，A、B、C是反比例函数y=下列说法中，正确的是（ ）
| A、相交的两条直线叫做垂直 |
| B、经过一点可以画两条直线 |
| C、平角是一条直线 |
| D、两条直线相交，只有一个交点 |
下列语句中错误的是（ ）
| A、数字0也是单项式 | ||||
B、
| ||||
| C、单项式-a的系数与次数都是 1 | ||||
D、-
|
下面的四个图形中，∠1与∠2是对顶角的是（ ）
A、 |
B、 |
C、 |
D、 |