题目内容
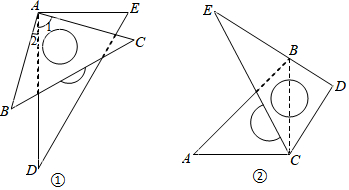
17．
如图，E为正方形ABCD的边CD上一点，将△BCE绕C点顺时针旋转90°后得到△DCF，则此时BE与DF的关系为相等且垂直．
分析 延长BE交DF于点G，由旋转知△BCE≌△DCF，即可得BE=DF、∠CDF=∠GBF，根据∠CDF+∠F=90°可得∠GBF+∠F=90°，从而得出答案．
解答 解：如图，延长BE交DF于点G，
由旋转变换的性质知：△BCE≌△DCF，
∴BE=DF，∠CDF=∠GBF；
∵∠CDF+∠F=90°，
∴∠GBF+∠F=90°，
∴BG⊥DF，
综上所述，BE与DF的关系为：相等且垂直．
故答案为：相等且垂直．
点评 主要考查了旋转变换的性质、正方形的性质、全等三角形的性质等知识点的应用问题；应牢固掌握旋转变换的性质、正方形的性质等知识点．
练习册系列答案
相关题目
某几何体的三视图及相关数据如图所示．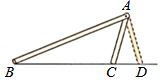
如图，△ABC与△ABD满足两边和其中一边的对角分别相等，即AB=AB，AC=AD，∠B=∠B，但△ABC与△ABD不全等，这说明有两边和其中一边的对角分别相等的两个三角形不一定全等．
2．
如图是一个长18cm，宽15cm的矩形图案，其中有两条宽度相等，互相垂直的彩条，彩条所占面积是图案面积的三分之一．设彩条的宽度为x cm，则下列方程正确的是（ ）
如图是一个长18cm，宽15cm的矩形图案，其中有两条宽度相等，互相垂直的彩条，彩条所占面积是图案面积的三分之一．设彩条的宽度为x cm，则下列方程正确的是（ ）| A． | 18x+15x-x2=$\frac{1}{3}$×15×18 | B． | （18-x）（15-x）=$\frac{1}{3}$×15×18 | ||
| C． | 18x+15x=$\frac{1}{3}$×15×18 | D． | 18x+15x+x2=$\frac{1}{3}$×15×18 |
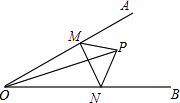如图，∠AOB=30°，点M、N分别是射线OB、OA上的动点，点P为∠AOB内一点，且OP=8，则△PMN的周长的最小值=8．