题目内容
如图,在△ABC上,点D、E分别是AC、BC边上的点,AE与BD交于点O,且CD=CE,∠1=∠2.
(1)求证:四边形ABDE是等腰梯形;
(2)若EC=2,BE=1,∠AOD=2∠1,求AB的长.


【考点】等腰梯形的判定.
【分析】(1)由等腰三角形的性质得出∠CDE=∠CED,由三角形的外角性质和已知条件得出∠AED=∠BDE,证出OD=OE,由AAS证明△AOD≌△BOE,得出AD=BE,OA=OB,由等腰三角形的性质得出∠OAB=∠OBA,再由对顶角相等和三角形内角和定理得出∠OAB=∠OBA=∠ODE=∠OED,证出DE∥AB,即可得出结论;
(2)由三角形的外角性质和已知条件得出∠1=∠OED,证出AD=ED=BE=1,由平行线的性质得出△CDE∽△CAB,得出对应边成比例,即可得出AB的长.
【解答】(1)证明:∵CD=CE,
∴∠CDE=∠CED,
∵∠CDE=∠2+∠AED,∠CED=∠1+∠BDE,∠1=∠2,
∴∠AED=∠BDE,
∴OD=OE,
在△AOD和△BOE中,
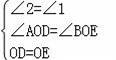
 ,
,
∴△AOD≌△BOE(AAS),
∴AD=BE,OA=OB,
∴∠OAB=∠OBA,
∵∠AOD=∠BOE,
∴∠OAB=∠OBA=∠ODE=∠OED,
∴DE∥AB,
∴四边形ABDE是等腰梯形;
(2)解:∵∠AOD=2∠1=∠ODE+∠OED,∠OED=∠ODE,
∴∠1=∠OED,
∴AD=ED=BE=1,
∵DE∥AB,
∴△CDE∽△CAB,
∴
 ,
,
即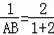
 ,
,
解得:AB=
 .
.
【点评】本题考查了等腰梯形的判定、等腰三角形的判定与性质、全等三角形的判定与性质、相似三角形的判定与性质等知识;熟练掌握等腰梯形的判定,证明三角形全等和三角形相似是解决问题的关键.

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案甲、乙两名同学某学期的四次数学测试成绩(单位:分)如下表:
| 第一次 | 第二次 | 第三次 | 第四次 | |
| 甲 | 87 | 95 | 85 | 93 |
| 乙 | 80 | 80 | 90 | 90 |
据上表计算,甲、乙两名同学四次数学测试成绩的方差分别为S甲2=17、S乙2=25,下列说法正确的是( )
A.甲同学四次数学测试成绩的平均数是89分
B.甲同学四次数学测试成绩的中位数是90分
C.乙同学四次数学测试成绩的众数是80分
D.乙同学四次数学测试成绩较稳定
 和
和 的图象交于点A(m,3),则不等式
的图象交于点A(m,3),则不等式 ≥
≥ 的解集是( )
的解集是( ) B、x≤3 C、x≤
B、x≤3 C、x≤ <
< ,则下列式子错误的是( )
,则下列式子错误的是( ) <
< B、
B、 <
< C、
C、 <
< D、
D、 <
<

 ,a﹣b=
,a﹣b=