题目内容
在△ABC中,∠A=50°,∠B,∠C的角平分线相交于点O,则∠BOC= .
考点:三角形内角和定理
专题:
分析:利用三角形的内角和定理以及角平分线的定义求∠BOC与∠A的关系,再把∠A代入即可求∠BOC的度数.
解答: 解:∵BO、CO分别平分∠ABC和∠ACB,
解:∵BO、CO分别平分∠ABC和∠ACB,
∴∠OBC=
∠ABC,∠OCB=
∠ACB,
∴∠BOC=180°-(∠OBC+∠OCB)
=180°-(
∠ABC+
∠ACB)
=180°-
(∠ABC+∠ACB)
=180°-
(180°-∠A)
=90°+
∠A.
当∠A=50°时,
∠BOC=90°+
∠A=90°+25°=115°.
故答案为:115°.
 解:∵BO、CO分别平分∠ABC和∠ACB,
解:∵BO、CO分别平分∠ABC和∠ACB,∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-(∠OBC+∠OCB)
=180°-(
| 1 |
| 2 |
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
当∠A=50°时,
∠BOC=90°+
| 1 |
| 2 |
故答案为:115°.
点评:本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
相关题目
下列说法正确的是( )
| A、某市“明天降雨的概率是75%”表示明天有75%的时间会降雨 | ||||
| B、随机抛掷一枚均匀的硬币,落地后正面一定朝上 | ||||
C、在一次抽奖活动中,“中奖的概率是
| ||||
D、从装有若干个除颜色外完全相同的红球和白球的口袋中,如果任意摸出一个红球的概率是
|
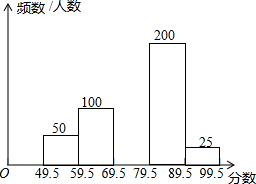 某市为了解参加历史科结业的2万名学生的考试成绩情况,现从中随机抽取部分学生的成绩作为一个样本,整理后分成5组,绘制了频数分布直方图,其中,第二组的频率为0.2.
某市为了解参加历史科结业的2万名学生的考试成绩情况,现从中随机抽取部分学生的成绩作为一个样本,整理后分成5组,绘制了频数分布直方图,其中,第二组的频率为0.2.