题目内容
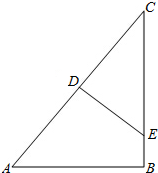 如图,在Rt△ABC中,∠B=90°,AC的垂直平分线DE交AC于点D,交BC于点E,若AC=8,DE=3,求BC的长度.
如图,在Rt△ABC中,∠B=90°,AC的垂直平分线DE交AC于点D,交BC于点E,若AC=8,DE=3,求BC的长度.考点:线段垂直平分线的性质,勾股定理
专题:
分析:连结AE.根据线段垂直平分线的性质可得AE=CE.在Rt△CDE中,利用勾股定理求出CE=
=5,则AE=CE=5,设BE=x,然后在Rt△ABC中,根据勾股定理得到AB2+BC2=AC2,依此列出方程52-x2+(x+5)2=82,解方程求出x的值,进而得到BC的值.
| 42+32 |
解答: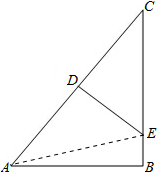 解:连结AE.
解:连结AE.
∵AC的垂直平分线DE交AC于点D,交BC于点E,
∴AE=CE,AD=CD=
AC=4.
在Rt△CDE中,∵∠CDE=90°,CD=4,DE=3,
∴CE=
=5,
∴AE=CE=5.
设BE=x,则BC=x+5.
在Rt△ABC中,∵∠B=90°,
∴AB2+BC2=AC2,
∴52-x2+(x+5)2=82,
解得x=1.4,
∴BC=1.4+5=6.4.
 解:连结AE.
解:连结AE.∵AC的垂直平分线DE交AC于点D,交BC于点E,
∴AE=CE,AD=CD=
| 1 |
| 2 |
在Rt△CDE中,∵∠CDE=90°,CD=4,DE=3,
∴CE=
| 42+32 |
∴AE=CE=5.
设BE=x,则BC=x+5.
在Rt△ABC中,∵∠B=90°,
∴AB2+BC2=AC2,
∴52-x2+(x+5)2=82,
解得x=1.4,
∴BC=1.4+5=6.4.
点评:本题考查了线段垂直平分线的性质:线段垂直平分线上任意一点,到线段两端点的距离相等.同时考查了勾股定理.

练习册系列答案
相关题目
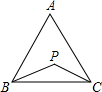 如图,在△ABC中,AB=AC,∠A=50°.如果P为三角形内一点,且∠PBC=∠PCA,那么∠BPC等于( )
如图,在△ABC中,AB=AC,∠A=50°.如果P为三角形内一点,且∠PBC=∠PCA,那么∠BPC等于( )| A、100° | B、115° |
| C、130° | D、65° |
 已知AB是⊙O的直径,弦CD和AB相交于P,∠APC=60°,BP=2,AP=8,求CD的长.
已知AB是⊙O的直径,弦CD和AB相交于P,∠APC=60°,BP=2,AP=8,求CD的长. 如图四边形ABCD,以AB为边作△ABM,使S△ABM=S四边形ABCD.
如图四边形ABCD,以AB为边作△ABM,使S△ABM=S四边形ABCD.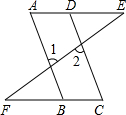 如图,请你从①∠1=∠2;②AD∥BC;③∠A=∠C;④∠ABF=∠E中,选取其中两个作为条件,一个作为结论,构成一个真命题,并加以证明.选取的条件是
如图,请你从①∠1=∠2;②AD∥BC;③∠A=∠C;④∠ABF=∠E中,选取其中两个作为条件,一个作为结论,构成一个真命题,并加以证明.选取的条件是