题目内容
4.计算题:(1)$\sqrt{12}$+$\frac{1}{\sqrt{3}}$-2$\sqrt{\frac{1}{3}}$
(2)4(x-2)2+2=27
(3)解方程组$\left\{\begin{array}{l}{3x+2y=4}\\{2x-y=5}\end{array}\right.$.
分析 (1)原式各项化为最简二次根式,合并即可得到结果;
(2)方程整理后,利用平方根定义开方即可求出解;
(3)方程组利用加减消元法求出解即可.
解答 解:(1)原式=2$\sqrt{3}$+$\frac{\sqrt{3}}{3}$-2×$\frac{\sqrt{3}}{3}$=$\frac{5\sqrt{3}}{3}$;
(2)方程整理得:(x-2)2=$\frac{25}{4}$,
开方得:x-2=±$\frac{5}{2}$,
解得:x1=$\frac{9}{2}$,x2=-$\frac{1}{2}$;
(3)$\left\{\begin{array}{l}{3x+2y=4①}\\{2x-y=5②}\end{array}\right.$,
①+②×2得:7x=14,即x=2,
把x=2代入②得:y=-1,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
15.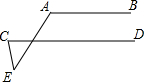 如图AB∥CD,∠E=40°,∠A=110°,则∠C的度数为( )
如图AB∥CD,∠E=40°,∠A=110°,则∠C的度数为( )
 如图AB∥CD,∠E=40°,∠A=110°,则∠C的度数为( )
如图AB∥CD,∠E=40°,∠A=110°,则∠C的度数为( )| A. | 60° | B. | 80° | C. | 75° | D. | 70° |
12.甲、乙两人参加学校组织的理化实验操作测试,近期的5次测试成绩如图所示.
(1)请你根据图中的数据填写表格:
(2)从平均数和方差相结合看,分析谁的成绩好些?从发展趋势来看,谁的成绩好些.

(1)请你根据图中的数据填写表格:
| 姓名 | 平均数 | 众数 | 方差 |
| 甲 | 8 | 8 | 0.4 |
| 乙 | 8 | 8 | 2.8 |
16.下列平面图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
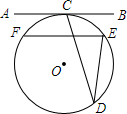 如图,直线AB与⊙O相切于点C,D是⊙O上的一点,∠CDE=22.5°,若EF∥AB,且EF=2,则⊙O的半径是$\sqrt{2}$.
如图,直线AB与⊙O相切于点C,D是⊙O上的一点,∠CDE=22.5°,若EF∥AB,且EF=2,则⊙O的半径是$\sqrt{2}$.