题目内容
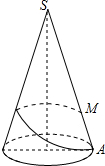 圆锥的底面半径为10cm,高为10
圆锥的底面半径为10cm,高为10| 5 |
(1)求圆锥的全面积.
(2)若一只小虫从底面上一点A出发,沿圆锥侧面绕行一周到母线SA上一点M处,且SM=3AM,求它所走的最短距离是多少.
考点:平面展开-最短路径问题,圆锥的计算
专题:
分析:(1)首先求得圆锥的母线长,然后求得展开扇形的弧长,进而求得其侧面积和底面积,从而求得其全面积;
(2)将圆锥的侧面展开,求得其展开扇形的圆心角的度数是90°,利用勾股定理求得AM的长即为最短距离.
(2)将圆锥的侧面展开,求得其展开扇形的圆心角的度数是90°,利用勾股定理求得AM的长即为最短距离.
解答:解:(1)由题意,可得圆锥的母线SA=
=10
(cm)
圆锥的侧面展开扇形的弧长l=2π•SA=20πcm
∴S侧=
L•SA=100
πcm2
S圆=πAO2=100πcm2,
∴S全=S圆+S底=(100
+100)π=100(
+1)π(cm2);
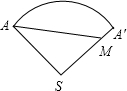 (2)沿母线SA将圆锥的侧面展开,如右图,则线段AM的长就是蚂蚁所走的最短距离
(2)沿母线SA将圆锥的侧面展开,如右图,则线段AM的长就是蚂蚁所走的最短距离
由(1)知,SA=10
cm,弧AA′=20πcm
∵
=20π,
∴∠S=n=60
°,
∵SA′=SA=40cm,SM=3A′M
∴SM=30cm,
∴在Rt△ASM中,由勾股定理得AM=50(cm)
所以,蚂蚁所走的最短距离是50cm.
| AO2+SO2 |
| 6 |
圆锥的侧面展开扇形的弧长l=2π•SA=20πcm
∴S侧=
| 1 |
| 2 |
| 6 |
S圆=πAO2=100πcm2,
∴S全=S圆+S底=(100
| 6 |
| 6 |
 (2)沿母线SA将圆锥的侧面展开,如右图,则线段AM的长就是蚂蚁所走的最短距离
(2)沿母线SA将圆锥的侧面展开,如右图,则线段AM的长就是蚂蚁所走的最短距离由(1)知,SA=10
| 6 |
∵
nπ×10
| ||
| 180 |
∴∠S=n=60
| 6 |
∵SA′=SA=40cm,SM=3A′M
∴SM=30cm,
∴在Rt△ASM中,由勾股定理得AM=50(cm)
所以,蚂蚁所走的最短距离是50cm.
点评:本题考查的是平面展开-最短路径问题,利用了勾股定理,弧长公式,圆的周长公式,等直角三角形的性质求解.难度适中.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 如图,菱形ABCD的对角线AC、BD相交于点O,AC=8,BD=6,点E为AB中点,连接OE,则OE的长是( )
如图,菱形ABCD的对角线AC、BD相交于点O,AC=8,BD=6,点E为AB中点,连接OE,则OE的长是( )| A、5 | ||
B、
| ||
| C、4 | ||
D、
|
甲、乙、丙三位同学在九年级上学期的五次数学测验中,他们的成绩的平均分都是90分(总分120分),方差分别是S甲2=15.7,S乙2=10.6,S丙2=13.2,则三人中成绩最稳定的是( )
| A、甲 | B、乙 | C、丙 | D、不能确定 |
 某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为60°,在教学楼三楼D处测得旗杆顶部的仰角为30°,旗杆底部与教学楼一楼在同一水平线上,已知CD=6米,则旗杆AB的高度为( )
某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为60°,在教学楼三楼D处测得旗杆顶部的仰角为30°,旗杆底部与教学楼一楼在同一水平线上,已知CD=6米,则旗杆AB的高度为( )| A、9米 | ||
B、9(1+
| ||
| C、12米 | ||
| D、18米 |
下列命题中,假命题是( )
| A、两点之间线段最短 |
| B、同角或等角的补角相等 |
| C、不相交的两条直线互相平行 |
| D、和为180°的两个角互为补角 |
 如图,⊙O的半径为4,点A、B、C在⊙O上,且∠ACB=45°,则弦AB的长是( )
如图,⊙O的半径为4,点A、B、C在⊙O上,且∠ACB=45°,则弦AB的长是( )A、4
| ||
| B、4 | ||
C、4
| ||
| D、3 |
在我校开展的“1116”读书活动中,九年级某班对学生5天内读书的情况做了抽查,统计如下:10,23,42,80,42(单位:页).这组数据的众数和中位数分别是( )
| A、36,42 |
| B、42,23 |
| C、42,36 |
| D、42,42 |
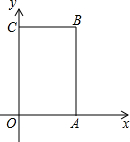 如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5).
如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5). 如图,点O是⊙O的圆心,点A、B、C在⊙O上,AO∥BC,∠AOB=42°,则∠OAC的度数是
如图,点O是⊙O的圆心,点A、B、C在⊙O上,AO∥BC,∠AOB=42°,则∠OAC的度数是