题目内容
 如图,点O是⊙O的圆心,点A、B、C在⊙O上,AO∥BC,∠AOB=42°,则∠OAC的度数是
如图,点O是⊙O的圆心,点A、B、C在⊙O上,AO∥BC,∠AOB=42°,则∠OAC的度数是考点:圆周角定理
专题:
分析:先根据圆周角定理求出∠ACB的度数,再由平行线的性质即可得出结论.
解答:解:∵∠AOB=42°,
∴∠ACB=
∠AOB=21°.
∵AO∥BC,
∴∠OAC=∠ACB=21°.
故答案为:21°.
∴∠ACB=
| 1 |
| 2 |
∵AO∥BC,
∴∠OAC=∠ACB=21°.
故答案为:21°.
点评:本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
下列算式错误的是( )
A、±
| |||
B、
| |||
C、-
| |||
D、
|
已知代数式3x2-6x+4的值为7,则代数式x2-2x+2的值为( )
| A、3 | B、4 | C、5 | D、6 |
分式方程
-
=0的解是( )
| 2 |
| x |
| 1 |
| x-1 |
| A、x=-2 | ||
| B、x=2 | ||
C、x=
| ||
| D、x=1 |

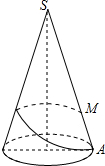 圆锥的底面半径为10cm,高为
圆锥的底面半径为10cm,高为 已知一次函数y=kx+b与y=mx+n的图象如图所示,若0<kx+b<mx+n,则x的取值范围为
已知一次函数y=kx+b与y=mx+n的图象如图所示,若0<kx+b<mx+n,则x的取值范围为 如图是我市交警在一个路口统计的某个时段来往车辆的车速情况.(单位:千米/时)
如图是我市交警在一个路口统计的某个时段来往车辆的车速情况.(单位:千米/时)