题目内容
11.如图1,在平面直角坐标系中,点O为坐标原点,抛物线y=mx2-6mx+5m与x轴交于A、B两点,与y轴交于点C,$\frac{AB}{OC}$=$\frac{4}{5}$.(1)求m的值;
(2)如图2,连接BC,点P为点B右侧的抛物线上一点,连接PA并延长交y轴于点D,过点P作PF⊥x轴于F,交线段CB的延长线于点E,连接DE,求证:DE∥AB;
(3)在(2)的条件下,点G在线段PE上,连接DG,若EG=2PG,∠DPE=2∠GDE时,求点P的坐标.

分析 (1)先求出A、B两点坐标,再根据条件求出点C坐标,即可解决问题.
(2)如图1中,设P(t,t2-6t+5),想办法求出D、E两点坐标(用t表示),只要纵坐标相同即可证明.
(3)如图3中,在DE上截取一点M,使得DM=MG.设P(t,t2-6t+5).则PE=t2-5t.,设DM=MG=a,在Rt△MGE中,a2=(t-a)2+[$\frac{2}{3}$(t2-5t)]2,求出a,再根据tan∠DPE=tan∠GME,得$\frac{DE}{PE}$=$\frac{EG}{EM}$,列出方程即可解决问题.
解答 解:(1)对于抛物线y=mx2-6mx+5m,
令y=0,得mx2-6mx+5m=0,解得x=1或5,
∴A(1,0),B(5,0),
∴AB=4,
∵$\frac{AB}{OC}$=$\frac{4}{5}$,
∴OC=5,
∴5m=5,
∴m=1.
(2)如图2中,设P(t,t2-6t+5).
∵OC=OB=5,∠AOB=90°,
∴∠OCB=∠OBC=∠EBF=45°,
∵PE⊥AB于F,
∴△BEF是等腰直角三角形,
∴BF=EF=t-5,
∴点E坐标(t,5-t),
∵A(1,0),P(t,t2-6t+5),
设直线AP的解析式为y=kx+b,则有$\left\{\begin{array}{l}{k+b=0}\\{tk+b={t}^{2}-6t+5}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=t-5}\\{b=5-t}\end{array}\right.$,
∴D(0,5-t),
∴D、E两点纵坐标相同,
∴DE∥AB.
(3)如图3中,在DE上截取一点M,使得DM=MG.设P(t,t2-6t+5).则PE=t2-5t.
∵EG=2PG,
∴GE=$\frac{2}{3}$(t2-5t),
∵MD=MG,设DM=MG=a,
∴∠MDG=∠MGD,
∴∠GME=2∠MDG,
∵∠DPE=2∠GDE,
∴∠DPE=∠GME,
∴tan∠DPE=tan∠GME,
∴$\frac{DE}{PE}$=$\frac{EG}{EM}$,
在Rt△MGE中,a2=(t-a)2+[$\frac{2}{3}$(t2-5t)]2,
∴a=$\frac{2}{9}$t3-$\frac{20}{9}$t2+$\frac{109}{18}$t,
∴EM=t-a=-$\frac{2}{9}$t3+$\frac{20}{9}$t2-$\frac{91}{18}$t,
∴$\frac{t}{{t}^{2}-5t}$=$\frac{\frac{2}{3}({t}^{2}-5t)}{-\frac{2}{9}{t}^{3}+\frac{20}{9}{t}^{2}-\frac{91}{18}t}$,
整理得到16t2-160t+391=0,
解得t=$\frac{23}{4}$或$\frac{17}{4}$(舍弃),
∴点P坐标($\frac{23}{4}$,$\frac{57}{16}$).
点评 本题考查二次函数综合题、一次函数、等腰直角三角形的性质、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,学会利用参数,构建方程解决问题,计算比较复杂,属于中考压轴题.

 名校课堂系列答案
名校课堂系列答案| A. | 3 | B. | -6 | C. | 6 | D. | -3 |
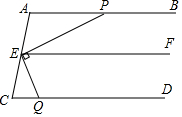 完成下面推理过程.在括号内的横线上填空或填上推理依据.
完成下面推理过程.在括号内的横线上填空或填上推理依据. 在Rt△ABC中,∠C=90°,若AB=20,AC=16,AD平分∠BAC交BC于点D,且BD:CD=5:4,则点D到线段AB的距离为$\frac{16}{3}$.
在Rt△ABC中,∠C=90°,若AB=20,AC=16,AD平分∠BAC交BC于点D,且BD:CD=5:4,则点D到线段AB的距离为$\frac{16}{3}$.