题目内容
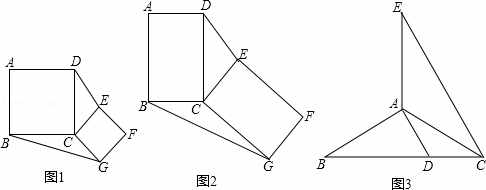
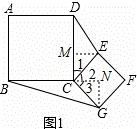
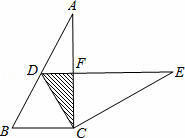
推理证明:如图1,在正方形ABCD和正方形CGFE中,连结DE、BG,设△DCE的面积为S1,△BCG的面积为S2,求证:S1=S2.
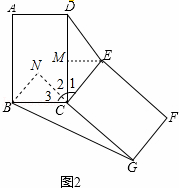
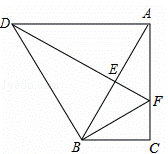
猜想论证:如图2,将矩形ABCD绕点C按顺时针方向旋转后得到矩形FECG,连结DE、BG,设△DCE的面积为S1,△BCG的面积为S2,猜想S1、S2的数量关系,并加以证明.
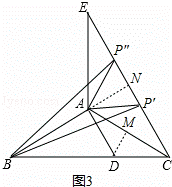
拓展探究:如图3,在△ABC中,AB=AC=10cm,∠B=30°,把△ABC沿AC翻折到△ACE,过点A作AD∥CE交BC于点D,在线段CE上存在点P,使△ABP的面积等于△ACD的面积,请你直接写出CP的长.
证明:如图1,过点E作EM⊥DC于M点,过点G作GN⊥BC交BC的延长线于N点,
∴∠EMC=∠N=90°,
∵四边形ABCD和四边形ECGF为正方形,
∴∠BCD=∠DCN=∠ECG=90°,CB=CD,CE=CG,
∴∠1=90°﹣∠2,∠3=90°﹣∠2,
∴∠1=∠3.
在△CME和△CNG中
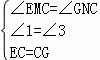
∴△CME≌△CNG(ASA).
∴EM=GN.
又∵S1=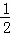 CD•EM,S2=
CD•EM,S2=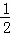 CB•GN,
CB•GN,
∴S1=S2;
猜想论证:
猜想:S1=S2,
证明:如图2,过点E作EM⊥DC于M,过点B作BN⊥GC交GC的延长线于点N,
∴∠EMC=∠N=90°,
∵矩形CGFE由矩形ABCD旋转得到的,
∴CE=CB,CG=CD,
∵∠ECG=∠ECN=∠BCD=90°,
∴∠1=90°﹣∠2,∠3=90°﹣∠2,∴∠1=∠3.
在△CME和△CNB中
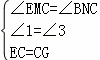
∴△CME≌△CNB(ASA).
∴EM=BN.
又∵S1=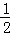 CD•EM,S2=
CD•EM,S2=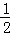 CG•BN,
CG•BN,
∴S1=S2;
拓展探究: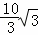 cm或
cm或 cm.
cm.
证明:如图3,作DM⊥AC于M,延长BA,交EC于N,
∵AB=AC=10cm,∠B=30°,
∴∠ACB=∠ABC=30°,
∴∠BAC=120°,
根据对折的性质,∠ACE=∠ACB=30°,
∵AD∥CE,
∴∠DAC=∠ACE=30°,
∴∠BAD=90° ,DM=
,DM=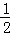 AD,
AD,
∴BN⊥EC,
∵AD=tan∠ABD•AB,AB=10cm,
∴AD=tan30°×10=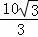 ,
,
∴DM=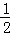 ×
×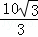 =
=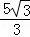 ,
,
∵S△ABP=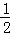 AB•PN,S△ADC=
AB•PN,S△ADC=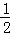 AC•DM,S△ABP=S△ADC,AB=AC,
AC•DM,S△ABP=S△ADC,AB=AC,
∴PN=DM=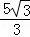 ,
,
在RT△ANC中∠ACN=30°,AC=10cm,
∴NC=cos∠ACN•AC=cos30°×10=5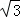 ,
,
∵在EC上到N的距离等于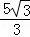 的点有两个,
的点有两个,
∴P′C=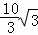 cm,P″C=
cm,P″C=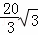 cm,
cm,
∴CP的长为: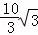 cm或
cm或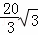 cm.
cm.

 AC的长为半径画弧,两弧相交于B,D两点,连接BD,AB,BC,CD,DA,以下结论:
AC的长为半径画弧,两弧相交于B,D两点,连接BD,AB,BC,CD,DA,以下结论:
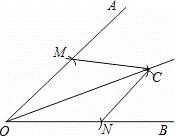
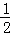 MN的长半径画弧,两弧在∠AOB内部相交于点C.
MN的长半径画弧,两弧在∠AOB内部相交于点C.