题目内容
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C旋转得到△EDC,使点D在AB边上,斜边DE交AC边于点F,则图中△CDF的面积为 .
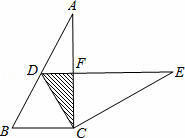
 解:∵△ABC是直角三角形,∠ACB=90°,∠A=30°,BC=2,
解:∵△ABC是直角三角形,∠ACB=90°,∠A=30°,BC=2,
∴∠B=60°,AC=BC×cot∠A=2× =2
=2  ,AB=2BC=4,
,AB=2BC=4,
∵△EDC是△ABC旋转而成,
∴BC=CD=BD= AB=2,
AB=2,
∵∠B=60°,
∴△BCD是等边三角形,
∴∠BCD=60°,
∴∠DCF=∠BCA﹣∠BCD=30°,
∵∠EDC=∠B=60°,
∴∠DFC=90°,
即DE⊥AC,
∴DE∥BC,
∵BD= AB=2,
AB=2,
∴DF是△ABC的中位线,
∴DF= BC=
BC= ×2=1,CF=
×2=1,CF= AC=
AC= ×2
×2  =
= ,
,
∴S△CDF= DF×CF=
DF×CF= ×
× =
= .
.
故答案为: .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

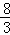 ),P点关于x轴的对称点为P2(a,b),则
),P点关于x轴的对称点为P2(a,b),则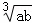 =( )
=( )
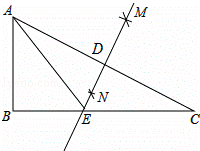
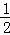 AC长为半径画弧,两弧相交于点M、N,连接MN,与AC、BC分别交于点D、E,连接AE.
AC长为半径画弧,两弧相交于点M、N,连接MN,与AC、BC分别交于点D、E,连接AE.