题目内容
19.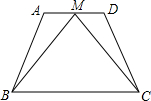 如图,梯形ABCD中,AD∥BC,点M是AD的中点,且MB=MC.若AD=4,AB=6,BC=8,则梯形ABCD的周长为24.
如图,梯形ABCD中,AD∥BC,点M是AD的中点,且MB=MC.若AD=4,AB=6,BC=8,则梯形ABCD的周长为24.
分析 先判断△AMB≌△DMC,从而得出AB=DC,然后代入数据即可求出梯形ABCD的周长.
解答 解:∵AD∥BC,
∴∠AMB=∠MBC,∠DMC=∠MCB,
又∵MC=MB,
∴∠MBC=∠MCB,
∴∠AMB=∠DMC,
在△AMB和△DMC中,
∵$\left\{\begin{array}{l}{AM=DM}\\{∠AMB=∠DMC}\\{MB=MC}\end{array}\right.$
∴△AMB≌△DMC(SAS),
∴AB=DC,
四边形ABCD的周长=AB+BC+CD+AD=24.
故选:24.
点评 此题考查了梯形、全等三角形的判定与性质,属于基础题,解答本题的关键是判断△AMB≌△DMC,得出AB=DC,难度一般.

练习册系列答案
相关题目
1.下列说法中正确的是( )
| A. | 9的平方根为3 | B. | $\frac{1}{\sqrt{2}}$化简后的结果是$\frac{\sqrt{2}}{2}$ | ||
| C. | $\sqrt{8}$最简二次根式 | D. | -27没有立方根 |
2.关于x的方程$\frac{3x-2}{x+2}$=2+$\frac{m}{x+2}$无解,则m的值为( )
| A. | -5 | B. | 5 | C. | -2 | D. | -8 |
7.1-6个月的婴儿生长发育得非常快,出生体重为4000克的婴儿,他们的体重y(克)和月龄x(月)之间的关系如表所示,则6个月大的婴儿的体重为( )
| 月龄/(月) | 1 | 2 | 3 | 4 | 5 |
| 体重/(克) | 4700 | 5400 | 6100 | 6800 | 7500 |
| A. | 7600克 | B. | 7800克 | C. | 8200克 | D. | 8500克 |
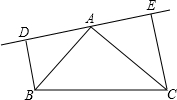 如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;若B,C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC.
如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;若B,C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC.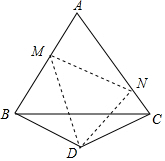 如图,△ABC是边长为10cm的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为20.
如图,△ABC是边长为10cm的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为20.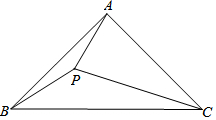 已知,如图,在△ABC中,AB=AC,∠BAC=α,且60°<α<120°,P是△ABC内部一点,且PC=AC,∠PCA=120°-α.
已知,如图,在△ABC中,AB=AC,∠BAC=α,且60°<α<120°,P是△ABC内部一点,且PC=AC,∠PCA=120°-α.
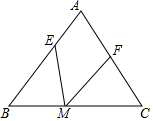 在△ABC中,AB=AC,BE=CM,BM=CF,∠EMF=50°,则∠A=80度.
在△ABC中,AB=AC,BE=CM,BM=CF,∠EMF=50°,则∠A=80度.