题目内容
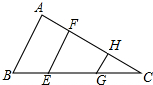如图，AB∥EF∥GH，BE=CG，求证：AB=EF+GH．考点：平行线分线段成比例
专题：证明题
分析：根据平行于三角形的一边，并且和其他两边（或两边的延长线）相交的直线，所截得的三角形的三边与原三角形的三边对应成比例，由HG∥AB得到△CHG∽△CAB，则
=
①；由EF∥AB得到△CFE∽△CAB，则
=
②，再把①与②相加，把CG用BE代换即可得到
=1．
| CG |
| CB |
| HG |
| AB |
| CE |
| CB |
| FE |
| AB |
| HG+EF |
| AB |
解答：证明：∵HG∥AB，
∴△CHG∽△CAB，
∴
=
①，
∵EF∥AB，
∴△CFE∽△CAB，
∴
=
②，
①+②得
=
，
∵BE=CG，
∴CG+CE=BE+CE=BC，
∴
=1，
∴AB=EF+GH．
∴△CHG∽△CAB，
∴
| CG |
| CB |
| HG |
| AB |
∵EF∥AB，
∴△CFE∽△CAB，
∴
| CE |
| CB |
| FE |
| AB |
①+②得
| CG+CE |
| CB |
| HG+EF |
| AB |
∵BE=CG，
∴CG+CE=BE+CE=BC，
∴
| HG+EF |
| AB |
∴AB=EF+GH．
点评：本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例；平行于三角形的一边，并且和其他两边（或两边的延长线）相交的直线，所截得的三角形的三边与原三角形的三边对应成比例．
练习册系列答案
相关题目
如图所示，在等腰△ABC中，AB=AC，∠BAC=36°，AE是△ABC的外角∠DAC的平分线，BF是∠ABC的平分线，BF的延长线交AE于E．
如图，四边形ABCD内接于⊙O，∠B=50°，∠ACD=25°，∠BAD=65°，求证：
已知：AB=BC=CA，BD=DE=BE，∠1=∠2=∠3，联结AE、DC，求证：AE=DC．