题目内容
 如图,在⊙O中,C、D是直径AB上两点,且AC=BD,MC⊥AB,ND⊥AB,M、N在⊙O上.
如图,在⊙O中,C、D是直径AB上两点,且AC=BD,MC⊥AB,ND⊥AB,M、N在⊙O上.(1)求证:
 |
| AM |
 |
| BN |
(2)若C、D分别为OA、OB中点,则
 |
| AM |
 |
| MN |
 |
| NB |
考点:圆心角、弧、弦的关系,全等三角形的判定与性质
专题:证明题
分析:(1)连结OM、ON,如图,由AC=BD易得OC=OD,则根据“HL”证明Rt△OCM≌Rt△ODN,得到∠AOM=∠BON,于是根据圆心角、弧、弦的关系得到
=
;
(2)由于C、D分别为OA、OB中点,则可得到OC=
OM,OD=
ON,根据含30度的直角三角形三边的关系得到∠OMC=30°,∠OND=30°,则∠MOC=∠NOD=60°,所以∠AOM=∠MON=∠BON,则利用圆心角、弧、弦的关系可得
=
=
.
 |
| AM |
 |
| BN |
(2)由于C、D分别为OA、OB中点,则可得到OC=
| 1 |
| 2 |
| 1 |
| 2 |
 |
| AM |
 |
| MN |
 |
| NB |
解答: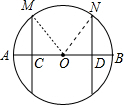 (1)证明:连结OM、ON,如图,
(1)证明:连结OM、ON,如图,
∵AC=BD,
∴OA-AC=OB-BD,即OC=OD,
∵MC⊥AB,ND⊥AB,
∴∠OCM=90°,∠ODN=90°,
在Rt△OCM和Rt△ODN中,
,
∴Rt△OCM≌Rt△ODN(HL),
∴∠AOM=∠BON,
∴
=
;
(2)解:
=
=
.理由如下:
∵C、D分别为OA、OB中点,
∴OC=
OA,OD=
OB,
∴OC=
OM,OD=
ON,
∴∠OMC=30°,∠OND=30°,
∴∠MOC=∠NOD=60°,
∴∠MON=60°,
∴∠AOM=∠MON=∠BON,
∴
=
=
.
 (1)证明:连结OM、ON,如图,
(1)证明:连结OM、ON,如图,∵AC=BD,
∴OA-AC=OB-BD,即OC=OD,
∵MC⊥AB,ND⊥AB,
∴∠OCM=90°,∠ODN=90°,
在Rt△OCM和Rt△ODN中,
|
∴Rt△OCM≌Rt△ODN(HL),
∴∠AOM=∠BON,
∴
 |
| AM |
 |
| BN |
(2)解:
 |
| AM |
 |
| MN |
 |
| NB |
∵C、D分别为OA、OB中点,
∴OC=
| 1 |
| 2 |
| 1 |
| 2 |
∴OC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OMC=30°,∠OND=30°,
∴∠MOC=∠NOD=60°,
∴∠MON=60°,
∴∠AOM=∠MON=∠BON,
∴
 |
| AM |
 |
| MN |
 |
| NB |
点评:本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了全等三角形的判定与性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列计算正确的是( )
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
 通过平移,可将图中的小猫移动到图( )
通过平移,可将图中的小猫移动到图( )A、 |
B、 |
C、 |
D、 |
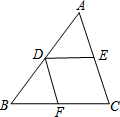 如图所示△ABC中,DE∥BC,DF∥AC,则下列比例式中正确的是( )
如图所示△ABC中,DE∥BC,DF∥AC,则下列比例式中正确的是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知反比例函数和正比例函数在第一象限的交点为A(1,3),则在第三象限的交点B为( )
| A、(-1,-3) |
| B、(-3,-1) |
| C、(-2,-6) |
| D、(-6,-2) |
反比例函数y=
图象上有三个点(-3,y1),(-1,y2),(2.y3),则y1,y2,y3的大小关系是( )
| 6 |
| x |
| A、y1<y2<y3 |
| B、y2<y1<y3 |
| C、y3<y1<y2 |
| D、y3<y2<y1 |
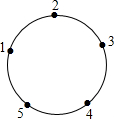 圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.若小明从编号为4的点开始,第2015次“移位”后,他到达编号为
圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.若小明从编号为4的点开始,第2015次“移位”后,他到达编号为 已知△ACD∽△BCA,若CD=4,CB=9,则AC=
已知△ACD∽△BCA,若CD=4,CB=9,则AC=