题目内容
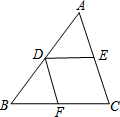如图所示△ABC中，DE∥BC，DF∥AC，则下列比例式中正确的是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：平行线分线段成比例
专题：
分析：根据平行于三角形的一边，并且和其他两边（或两边的延长线）相交的直线，所截得的三角形的三边与原三角形的三边对应成比例，由DE∥BC得到
=
，则可对A、C进行判断；根据平行线分线段成比例定理，由DE∥BC得
=
，由DF∥AC得
=
，所以
=
，则可对B进行判断；接着判断四边形DFCE为平行四边形得到CF=DE，所以
=
=
，于是可对D选项进行判断．
| AE |
| AC |
| DE |
| BC |
| AE |
| EC |
| AD |
| DB |
| CF |
| FB |
| AD |
| DB |
| AE |
| EC |
| CF |
| FB |
| CF |
| BC |
| DE |
| BC |
| AE |
| AC |
解答：解：∵DE∥BC，
∴
=
，所以A、C选项错误；
∵DE∥BC，
∴
=
，
∵DF∥AC，
∴
=
，
∴
=
，所以B选项正确；
∵DE∥BC，DF∥AC，
∴四边形DFCE为平行四边形，
∴CF=DE，
∴
=
=
，所以D选项错误．
故选B．
∴
| AE |
| AC |
| DE |
| BC |
∵DE∥BC，
∴
| AE |
| EC |
| AD |
| DB |
∵DF∥AC，
∴
| CF |
| FB |
| AD |
| DB |
∴
| AE |
| EC |
| CF |
| FB |
∵DE∥BC，DF∥AC，
∴四边形DFCE为平行四边形，
∴CF=DE，
∴
| CF |
| BC |
| DE |
| BC |
| AE |
| AC |
故选B．
点评：本题考查了平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例；平行于三角形的一边，并且和其他两边（或两边的延长线）相交的直线，所截得的三角形的三边与原三角形的三边对应成比例．
练习册系列答案
名校课堂系列答案
相关题目
如图所示，二次函数y=ax2与一次函数y=-ax+a的图象大致是（ ）
A、 |
B、 |
C、 |
D、 |
如图，在⊙O中，C、D是直径AB上两点，且AC=BD，MC⊥AB，ND⊥AB，M、N在⊙O上．
下列图形中，能通过折叠围成一个三棱柱的是（ ）
A、 |
B、 |
C、 |
D、 |
如图，在△ABC中，DE∥BC，∠A=55°，∠B=70°，则∠AED=（ ）| A、55° | B、70° |
| C、125° | D、50° |