题目内容
5．若α、b、c是△ABC的三边长且满足a2-6a+b2-8b+$\sqrt{c-5}$+25=0．请根据已知条件判断其形状．分析 把25分成9、16，然后与（a2-6a）、（b2-8b）分别组成完全平方公式，再利用非负数的性质，可分别求出a、b、c的值，然后利用勾股定理可证△ABC是直角三角形．
解答 解：∵a2-6a+b2-8b+$\sqrt{c-5}$+25=0，
∴a2-6a+9+b2-8b+16+$\sqrt{c-5}$=0，
即（a-3）2+（b-4）2+$\sqrt{c-5}$=0，
∴a=3，b=4，c=5，
∵32+42=52，
∴△ABC是直角三角形．
点评 此题考查了配方法的应用、勾股定理、非负数的性质，解题的关键是注意配方法的步骤，在变形的过程中不要改变式子的值．
练习册系列答案
相关题目
15．A（-3，2）关于y轴的对称点是B，B关于x轴的对称点是C，则点C的坐标是（ ）
| A． | （-2，3） | B． | （-3，2） | C． | （3，-2） | D． | （3，2） |
16．
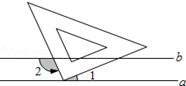如图，小华把三角板的直角顶点放在直线a上，两条直角边与直线b相交，如果a∥b，且∠1=40°，则∠2的度数为（ ）
如图，小华把三角板的直角顶点放在直线a上，两条直角边与直线b相交，如果a∥b，且∠1=40°，则∠2的度数为（ ）| A． | 100° | B． | 110° | C． | 120° | D． | 130° |
如图，△ABC是⊙O的内接三角形，∠A=30°，BC=2cm，求⊙O的半径．