题目内容
19. 已知:如图,△ABC为等边三角形,点B在线段DE上,∠ADB=∠E=60°,求证:BD=EC.
已知:如图,△ABC为等边三角形,点B在线段DE上,∠ADB=∠E=60°,求证:BD=EC.
分析 利用等边三角形的性质和三角形的内角和得出∠BAD=∠CBE,证得△ABD≌△BCE,得出结论.
解答 证明:∵△ABC是等边三角形
∴AB=BC,∠ABC=60゜,
∵∠ABC=60゜,
∴∠ABD+∠CBE=180゜-60゜=120゜,
在△ABD中,∠ADB=60゜,
∴∠BAD+∠ABD=180゜-60゜=120゜,
∵∠ABD+∠CBE=120゜,∠BAD+∠ABD=120゜,
∴∠BAD=∠CBE,
在△ABD和△BCE中,
$\left\{\begin{array}{l}{∠ADB=∠E}\\{∠DAB=∠EBC}\\{AB=BC}\end{array}\right.$,
∴△ABD≌△BCE,
∴BD=EC.
点评 本题主要考查了全等三角形的判定及性质,等边三角形的性质,掌握三角形全等的判定方法是解决问题的关键.

练习册系列答案
相关题目
4.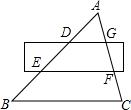 如图,△ABC被一平行于BC的矩形所截,AB被截成三等分,若△ADG的面积为a,则图中四边形DEFG的面积是( )
如图,△ABC被一平行于BC的矩形所截,AB被截成三等分,若△ADG的面积为a,则图中四边形DEFG的面积是( )
 如图,△ABC被一平行于BC的矩形所截,AB被截成三等分,若△ADG的面积为a,则图中四边形DEFG的面积是( )
如图,△ABC被一平行于BC的矩形所截,AB被截成三等分,若△ADG的面积为a,则图中四边形DEFG的面积是( )| A. | a | B. | 2a | C. | 3a | D. | 4a |
11.下列四个命题中,真命题有( )
①两条直线被第三条直线所截,内错角相等.
②如果∠1和∠2是对顶角,那么∠1=∠2.
③0.3,0.4,0.5是一组勾股数.
④如果x2>0,那么x>0.
①两条直线被第三条直线所截,内错角相等.
②如果∠1和∠2是对顶角,那么∠1=∠2.
③0.3,0.4,0.5是一组勾股数.
④如果x2>0,那么x>0.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.某工厂生产一种螺丝帽,要求是:螺丝帽内径可有0.02毫米的误差,先抽查6个螺丝帽,检查结果如下:
请问:这6个螺丝帽中符合要求的有几个?
| 1 | 2 | 3 | 4 | 5 | 6 |
| +0.031 | -0.017 | +0.023 | +0.013 | -0.021 | -0.019 |
 如图是一盘中国象棋残局的一部分,以“帅”为原点建立坐标系,知道“兵”所在位置的坐标是(2,3),则“炮”所在位置的坐标是(-3,2).
如图是一盘中国象棋残局的一部分,以“帅”为原点建立坐标系,知道“兵”所在位置的坐标是(2,3),则“炮”所在位置的坐标是(-3,2). 如图,已知Rt△ABC≌Rt△DEC,连结AD,若∠1=25°,则∠B的度数是70°.
如图,已知Rt△ABC≌Rt△DEC,连结AD,若∠1=25°,则∠B的度数是70°. 如图所示,PA、PB是⊙O的切线,A、B为切点,∠APB=40°,点C是⊙O上不同于A、B的任意一点,则∠ACB的度数为70°或110°.
如图所示,PA、PB是⊙O的切线,A、B为切点,∠APB=40°,点C是⊙O上不同于A、B的任意一点,则∠ACB的度数为70°或110°.