题目内容

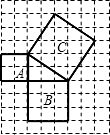精英家教网如图，正方形A的面积是4，正方形B的面积是9，则正方形C的边长是
 
．
分析：设正方形A的边长是a，正方形B的边长是b，正方形C的边长是c，可根据勾股定理表示出三边关系．
解答：解：∵a2+b2=c2，
∴c2=4+9=13．
c=
13
．
故答案为：
13
．
点评：本题考查勾股定理，根据勾股定理可求出边长．
练习册系列答案
相关题目
精英家教网如图，正方形OABC的面积是4，点B在反比例函数y=
kx
（k＞0，x＜0）的图象上．若点R是该反比例函数图象上异于点B的任意一点，过点R分别作x轴、y轴的垂线，垂足为M、N，从矩形OMRN的面积中减去其与正方形OABC重合部分的面积，记剩余部分的面积为S，则当S=m（m为常数，且0＜m＜4）时，点R的坐标是
 
．（用含m的代数式表示）
精英家教网如图，正方形A的面积是
 
．
精英家教网如图，正方形OABC的面积是9，点O为坐标原点，点A在x轴上，点C在y轴上，点B、点P（m，n）在函数y=
k
x
（k＞0，x＞0）的图象上．过点P分别作x轴、y轴的垂线，垂足为E、F．
（1）求B点坐标和k的值；
（2）当P点的横坐标大于B点的横坐标，且S四边形AEPG=
9
2
时，求PA所在的直线方程；
（3）求函数y=m+n的最小值；
（注：可使用如下平均值定理：若a＞0，b＞0，则a+b≥2
ab
，当且仅当a=b时等号成立．）
如图，正方形OABC的面积为9，点O为坐标原点，点B在函数y=
k
x
（k＞0，x＞0）的图象上，点P（m、n）是函数y=
k
x
（k＞0，x＞0）图象上的一个动点，过点P分别作x轴、y轴的垂线，垂足分别为E、F，并设两个四边形OEPF和OABC不重合部分的面积之和为S．
（1）求B点坐标和k的值；
（2）当S=
9
2
时，求点P的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网