题目内容
14. 如图,在⊙O中,直径AB⊥CD,AB与CD相交于点E,连接AC,BC,点F是BA延长线上的一点,且∠FCA=∠B.
如图,在⊙O中,直径AB⊥CD,AB与CD相交于点E,连接AC,BC,点F是BA延长线上的一点,且∠FCA=∠B.(1)求证:CF是⊙O的切线;
(2)若AE=4,tan∠ACD=$\frac{\sqrt{3}}{3}$,求FC的长.
分析 (1)欲证明CF是⊙O的切线,只要证明OC⊥CF即可.
(2)通过计算发现AE=OE,因为CE⊥OA,可以证明△AOC是等边三角形,由此即可解决问题.
解答 (1)证明:如图,连接OC.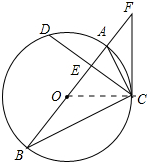 ∵AB是直径,
∵AB是直径,
∴∠ACB=90°,
∵OB=OC,
∴∠B=∠OCB,
∴∠OCB+∠ACO=90°,
∵∠FCA=∠B,
∴∠FCA+∠ACO=90°,即∠FCO=90°,
∴FC⊥OC,
∴FC是⊙O切线.
(2)解:∵AB⊥CD,
∴∠AEC=90°,
∵tan∠ACE=$\frac{\sqrt{3}}{3}$=$\frac{AE}{EC}$,AE=4,
∴EC=4$\sqrt{3}$,设OA=OC=r,
在RT△OEC中,r2=(r-4)2+(4$\sqrt{3}$)2,
∴r=8,
∴OE=AE=4,∵CE⊥OA,
∴CA=CO=8,
∴△AOC是等边三角形,
∴∠FOC=60°,
在RT△FOC中,∵∠OCF=90°,OC=8,∠F=30°,
∴OF=16,CF=$\sqrt{O{F}^{2}-O{C}^{2}}$=8$\sqrt{3}$.
点评 本题考查切线的判定、三角函数、勾股定理.等边三角形的判定和性质、直角三角形30度角性质,解题的关键是灵活运用直线知识解决问题,证明△AOC是等边三角形是解决问题的突破口,属于中考常考题型.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
6.下列命题错误的是( )
| A. | 平行四边形的对角线互相平分 | |
| B. | 对角线互相垂直平分的四边形是菱形 | |
| C. | 矩形的对角线相等 | |
| D. | 对角线相等的四边形是正方形 |
4. 如图,矩形ABCD和矩形CEFG中,AD=2,AB=1,CE=3,EF=6,连接AF,H是AF的中点,那么CH的长是( )
如图,矩形ABCD和矩形CEFG中,AD=2,AB=1,CE=3,EF=6,连接AF,H是AF的中点,那么CH的长是( )
 如图,矩形ABCD和矩形CEFG中,AD=2,AB=1,CE=3,EF=6,连接AF,H是AF的中点,那么CH的长是( )
如图,矩形ABCD和矩形CEFG中,AD=2,AB=1,CE=3,EF=6,连接AF,H是AF的中点,那么CH的长是( )| A. | $\frac{5}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{5}{2}$$\sqrt{2}$ | D. | 2 |
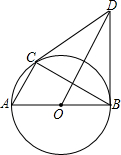 如图,⊙O是Rt△ABC的外接圆,点O在AB上,BD⊥AB,点B是垂足,OD∥AC,连接CD.
如图,⊙O是Rt△ABC的外接圆,点O在AB上,BD⊥AB,点B是垂足,OD∥AC,连接CD.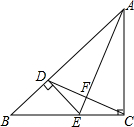 已知,如图,△ABC中,AC=BC,∠C=90°,AE平分∠BAC交BC于E,过E做ED⊥AB于D,连接DC交AE于F,其中BD=1.则在下列结论中:①AE⊥DC;②AB=2+$\sqrt{2}$;③$\frac{AE}{CD}$=2;④AE•CD=2+2$\sqrt{2}$.其中正确的结论是①②④.
已知,如图,△ABC中,AC=BC,∠C=90°,AE平分∠BAC交BC于E,过E做ED⊥AB于D,连接DC交AE于F,其中BD=1.则在下列结论中:①AE⊥DC;②AB=2+$\sqrt{2}$;③$\frac{AE}{CD}$=2;④AE•CD=2+2$\sqrt{2}$.其中正确的结论是①②④. 如图,在矩形ABCD中,AB=2,BC=4,M是AD的中点,动点E在线段AB上,连结EM并延长交射线CD于点F,过点M作EF的垂线交BC于点G,连结EG、FG.
如图,在矩形ABCD中,AB=2,BC=4,M是AD的中点,动点E在线段AB上,连结EM并延长交射线CD于点F,过点M作EF的垂线交BC于点G,连结EG、FG.