题目内容
14. 己知数轴上顺次有A,B,C三点,分别表示数a,b,c,并且满足(a+24)2+|b+10|=0,b与c互为相反数,两只电子小蜗牛甲、乙分别从A,C两点同时相向而行,甲的速度为2个单位/秒,乙的速度为6个单位/秒.
己知数轴上顺次有A,B,C三点,分别表示数a,b,c,并且满足(a+24)2+|b+10|=0,b与c互为相反数,两只电子小蜗牛甲、乙分别从A,C两点同时相向而行,甲的速度为2个单位/秒,乙的速度为6个单位/秒.(])求A,B,C三点分别表示的数;
(2)运动多少秒时,甲,乙到B的距离相等;
(3)设点P在数轴上,表示的数为-21,若甲运动到点P时立即掉头返回,问甲,乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由.
分析 (1)首先由非负数的性质求得a=-24,b=-10;然后由相反数的定义求得c=10;
(2)设运动x秒时,甲、乙到点B的距离相等,分都不过点B和都过点B,列出方程解答即可;
(3)设运动a秒时,甲、乙还能在数轴上相遇,分别表示出甲走的路程与乙走的路程,利用路程差为34,列出方程解答即可.
解答 解:(1)∵(a+24)2+|b+10|=0,
∴a+24=0,b+10=0,
解得a=-24,b=-10.
又∵b与c互为相反数,
∴c=10,
∴A、B、C三点分别表示的数是-24,-10,10;
(2)易知AB=14,BC=20.
设运动x秒时,甲、乙到点B的距离相等.则依题意,得
当都不到点B,14-2x=20-6x,
解得x=1.5.
当都过B点时,2x-14-10=10-(6x-20)
解得:x=6.75
答:运动1.5s或6.75s时,甲、乙到点B的距离相等;
(3)能.
由题意得AP=3,
设运动a秒时,甲、乙还能在数轴上相遇,由题意得
2(a-3×2÷2)+34=6a
解得:a=7
所以甲,乙还能在数轴上相遇.
点评 此题考查一元一次方程的实际运用,借助数轴,利用行程问题中的基本数量关系解决问题.

练习册系列答案
相关题目
2.等边三角形PHK和正方形PQRS内接于圆PQHRKS,则∠KHS等于 ( )
| A. | 15° | B. | 22.5° | C. | 30° | D. | 37.5° |
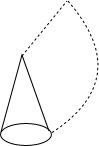 (1)已知圆锥的底面半径为2cm,母线长为4cm,求圆锥的表面积;
(1)已知圆锥的底面半径为2cm,母线长为4cm,求圆锥的表面积;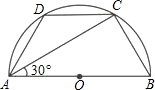 如图,已知在半圆AOB中,AD=DC,∠CAB=30°,AB=8,求AD的长.
如图,已知在半圆AOB中,AD=DC,∠CAB=30°,AB=8,求AD的长. 如图所示,在没有标出原点的数轴上A,B,C,D四点对应的有理数都是整数,且其中一个位于原点的位置,若A,B对应的有理数a,b满足a+b=-5,那么数轴的原点只能是A,B,C,D四点中的哪个点?为什么?
如图所示,在没有标出原点的数轴上A,B,C,D四点对应的有理数都是整数,且其中一个位于原点的位置,若A,B对应的有理数a,b满足a+b=-5,那么数轴的原点只能是A,B,C,D四点中的哪个点?为什么?