题目内容

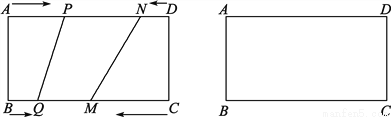
如图，在矩形ABCD中，BC＝20 cm，P，Q，M，N分别从A，B，C，D出发，沿AD，BC，CB，DA方向在矩形的边上同时运动，当有一个点先到达所在运动边的另一个端点时，运动即停止．已知在相同时间内，若BQ＝x cm(x≠0)，则AP＝2x cm，CM＝3x cm，DN＝x2 cm，

(1)当x为何值时，点P，N重合；

(2)当x为何值是，以P，Q，M，N为顶点的四边形是平行四边形．

(1) 当时，P，N重合;(2) 当x＝2或x＝4时，以P，Q，M，N为顶点的四边形是平行四边形. 【解析】试题分析：（1）当P、N重合时有：AP+DN= 20,解方程可得. (2)MQ=PN,时PQMN是平行四边形,其中不确定P，N的位置关系，所以需要分类讨论. 试题解析： (1)当P、N重合时有：AP+DN=AD=20, 即：x2+2x-20=0，解得： （舍去）...
练习册系列答案
相关题目

下列四个几何体中，从上面看得到的平面图形是四边形的是( )

A. B. C. D.

D 【解析】试题解析：A. 从上面看得到的平面图形是圆，故该选项错误； B. 从上面看得到的平面图形是三角形，故该选项错误； C. 从上面看得到的平面图形是三角形，故该选项错误； D. 从上面看得到的平面图形是四边形，正确. 故选D.

从－，0， ，π，3.5这五个数中，随机抽取一个，则抽到无理数的概率是__ _．

【解析】根据无理数的意义和特点，可知无理数有－和π，故可求得抽到无理数的概率是. 故答案为： .

如图，矩形ABCD的一边BC与⊙O相切于G，DC=6，且对角线BD经过圆心O，AD交⊙O于点E，连接BE，BE恰好是⊙O的切线，已知点P在对角线BD上运动，若以B、P、G三点构成的三角形与△BED相似，则BP=______．

4或12． 【解析】连接OE、OG、DG，如图，GO的延长线交AD于H， ∵BE和BG为⊙O的切线， ∴BG=BE，OB平分∠GBE，OG⊥BC， 而BC∥AD， ∴GH⊥AD， ∴EH=DH， 易得四边形CDHG为矩形， ∴CG=DH， ∴DE=2CG， ∵∠EDB=∠CBD， ∴∠EBD=∠EDB， ∴EB=ED， ...

如图，在坐标系中，以A（0，2）为位似中心，在y轴右侧作△ABC放大2倍后的位似图形△AB'C'，若C的对应点C'的坐标为（m，n），则点C的坐标为（　　）

A. （m， n+3） B. （m， n﹣3）

C. （m， n+2） D. （m， n﹣2）

A 【解析】过点A作x轴的平行线DD′，作CD⊥DD′于D，作C′D′⊥DD′于D′， 设C（x，y）， 则CD=y﹣2、AD=﹣x，C′D′=2﹣n，AD′=m， ∵△ABC与△AB′C′的位似比为2：1， ∴,, 解得：x=﹣m，y=﹣n+3， ∴点C的坐标为（﹣m，﹣n+3）， 故选A．

是一元二次方程x2－2x＋1＝0的根．

求代数式 ÷(x＋2－)的值．

. 【解析】试题分析：化简分式，再求出一元二次方程的根，代入求值. 试题解析： 由x2－2x＋1＝0得：x=1, ∴原式=, 当x=1时，原式=.

若一元二次方程x2＋2x＋m＝0有实数根，则m的取值范围是 (　　)

A. m≤－1 B. m≤1

C. m≤4 D. m≤

B 【解析】试题分析：∵一元二次方程x2+2x+m=0有实数解， ∴b2-4ac=22-4m≥0， 解得：m≤1， 则m的取值范围是m≤1． 故选：B．

如图，在平面直角坐标系xOy中，正比例函数y＝kx的图象与反比例函数的图象有一个交点为A(m，2)．

(1)求m的值及正比例函数y＝kx的表达式；

(2)试判断点B(2，3)是否在正比例函数图象上，并说明理由．

(1)m＝1，正比例函数的表达式为y＝2x；(2)点B(2，3)不在正比例函数图象上，理由见解析． 【解析】试题分析：（1）将A（m，2）点代入反比例函数y= y＝，即可求得m的值； （2）将A点坐标代入正比例函数y=kx，即可求得正比例函数的解析式； （3）将x=2代入（2）中所求的正比例函数的解析式，求出对应的y值，然后与3比较，如果y=3，那么点B（2，3）是否在正比例函数...

如图，线段AB是⊙O的直径，弦CD丄AB，∠CAB=20°，则∠BOD等于（　　）

A. 20° B. 30° C. 40° D. 60°

C 【解析】试题分析：由线段AB是⊙O的直径，弦CD丄AB，根据垂径定理的即可求得： ，然后由圆周角定理可得∠BOD=2∠CAB=2×20°=40°． 故选：C．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网