题目内容
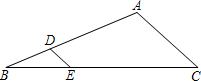
10. 如图,在△ABC中,AD平分∠CAB交BC于点D,过点C作CE⊥AD于E,CE的延长线交AB于点F,点G是BF的中点,连接EG.
如图,在△ABC中,AD平分∠CAB交BC于点D,过点C作CE⊥AD于E,CE的延长线交AB于点F,点G是BF的中点,连接EG.(1)求证:EG∥BC;
(2)若△ACD∽△AEC,且AE•AD=16,AB=4$\sqrt{5}$,求EG的长.
分析 (1)先证明△ACE≌△AFE,然后可得到CE=EF,故此可证明EG是△FBC的中位线,从而可证明EG∥BC;
(2)由相似三角形的性质可知AC 2=AE•AD=16,从而可求得AC=4,然后在Rt△ABC中,由勾股定理可求得BC=8,最后依据三角形的中位线定理可求得EG=4.
解答 证明:(1)∵AD平分∠CAB,
∴∠CAE=∠FAE.
∵CE⊥AD,
∴∠CEA=∠FEA=90°.
在△ACE和△AFE中,
$\left\{\begin{array}{l}{∠CAE=∠FAE}\\{AE=AE}\\{∠CEA=∠FEA=90°}\end{array}\right.$,
∴△ACE≌△AFE.
∴CE=FE.
又∵G是BF的中点,
∴EG∥BC.
(2)∵△ACD∽△AEC,CE⊥AD,
∴∠ACD=∠AEC=90°,且$\frac{AC}{AD}=\frac{AE}{AC}$.
∴AC 2=AE•AD=16.
∴AC=4.
在Rt△ABC中,AB=4$\sqrt{5}$,AC=4,由勾股定理得:BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{80-16}$=8.
∵EG是△FBC的中位线,
∴EG=$\frac{1}{2}BC=\frac{1}{2}×8=4$.
点评 本题主要考查的是相似三角形的性质、全等三角形的性质和判定、勾股定理、三角形的中位线定理,证得EG是△FBC的中位线是解题的关键.

练习册系列答案
相关题目
20.已知点(x1,y1),(x2,y2)是函数y=(m-3)x2图象上的两点,且0<x1<x2当时,有y1<y2,则m的取值范围是( )
| A. | m>3 | B. | m≥3 | C. | m<3 | D. | m≤3 |
1.下列式子不是二次根式的是( )
| A. | $\sqrt{5}$ | B. | $\sqrt{{a^2}+1}$ | C. | $\sqrt{1.2}$ | D. | $\sqrt{-|x|-1}$ |
19.在有理数:-2,-(-2),|-2|,-|+2|,-|-2|,+(-2),-(+2)中负数有( )
| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
 如图,在△ABC中,DE∥AC,$\frac{BD}{DA}=\frac{1}{2}$,DE=3,则AC的长为( )
如图,在△ABC中,DE∥AC,$\frac{BD}{DA}=\frac{1}{2}$,DE=3,则AC的长为( )