题目内容
18.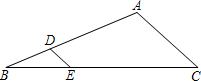 如图,在△ABC中,DE∥AC,$\frac{BD}{DA}=\frac{1}{2}$,DE=3,则AC的长为( )
如图,在△ABC中,DE∥AC,$\frac{BD}{DA}=\frac{1}{2}$,DE=3,则AC的长为( )| A. | 3 | B. | 4 | C. | 6 | D. | 9 |
分析 由$\frac{BD}{DA}=\frac{1}{2}$可知$\frac{DB}{AB}=\frac{1}{3}$,由DE∥AC可知△BDE∽△BAC,然后根据相似三角形的性质可求得AC的长.
解答 解:∵$\frac{BD}{DA}=\frac{1}{2}$,
∴$\frac{DB}{AB}=\frac{1}{3}$.
∵DE∥AC,
∴△BDE∽△BAC.
∴$\frac{ED}{AC}=\frac{BD}{BA}$,即$\frac{3}{AC}=\frac{1}{3}$.
解得:AC=9.
故选:D.
点评 本题主要考查的是相似三角形的性质和判定,证得△BDE∽△BAC是解题的关键.

练习册系列答案
相关题目
8. 如图,△ABC中,CD和BE都是高,则图中互余的角度有( )
如图,△ABC中,CD和BE都是高,则图中互余的角度有( )
 如图,△ABC中,CD和BE都是高,则图中互余的角度有( )
如图,△ABC中,CD和BE都是高,则图中互余的角度有( )| A. | 4对 | B. | 5对 | C. | 6对 | D. | 以上均不对 |
 已知:如图,AB=AC=12cm,AB的垂直平分线分别交AC、AB 于D、E,△ABE的周长等于29cm,则EC的长为3.5cm.
已知:如图,AB=AC=12cm,AB的垂直平分线分别交AC、AB 于D、E,△ABE的周长等于29cm,则EC的长为3.5cm. 如图,细心观察图形,认真分析各式,然后再解答问题.${(\sqrt{1})}^{2}$+1=2,S1=$\frac{\sqrt{1}}{2}$${(\sqrt{2})}^{2}$+1=3,S2=$\frac{\sqrt{2}}{2}$${(\sqrt{2})}^{2}$+1=4,S3=$\frac{\sqrt{3}}{2}$
如图,细心观察图形,认真分析各式,然后再解答问题.${(\sqrt{1})}^{2}$+1=2,S1=$\frac{\sqrt{1}}{2}$${(\sqrt{2})}^{2}$+1=3,S2=$\frac{\sqrt{2}}{2}$${(\sqrt{2})}^{2}$+1=4,S3=$\frac{\sqrt{3}}{2}$ 如图,在△ABC中,AD平分∠CAB交BC于点D,过点C作CE⊥AD于E,CE的延长线交AB于点F,点G是BF的中点,连接EG.
如图,在△ABC中,AD平分∠CAB交BC于点D,过点C作CE⊥AD于E,CE的延长线交AB于点F,点G是BF的中点,连接EG.