题目内容
已知△ABC是等腰直角三角形,∠C=90°,直角边的长为2,把点A沿MN折叠,点A恰好与BC边的中点D重合,则重叠部分即△MND的面积= .
考点:翻折变换(折叠问题)
专题:
分析:设AD与MN交于点P,作DE⊥AB于E.先在等腰直角三角形△ABC中,利用勾股定理求出AB=2
,根据折叠的性质及已知条件得到MN垂直平分AD,△AMN≌△DMN,CD=BD=1,在Rt△ACD中,利用勾股定理求出AD=
=
,于是AP=DP=
.再证明△APM∽△ACD,由相似三角形对应边成比例求出PM=
,由△BED为等腰直角三角形,得出BE=DE=
BD=
,则AE=AB-BE=
,由△APN∽△AED,根据相似三角形对应边成比例求出PN=
,于是MN=PM+PN=
,然后根据△MND的面积=
MN•DP,代入数值计算即可求解.
| 2 |
| AC2+CD2 |
| 5 |
| ||
| 2 |
| ||
| 4 |
| ||
| 2 |
| ||
| 2 |
3
| ||
| 2 |
| ||
| 6 |
5
| ||
| 12 |
| 1 |
| 2 |
解答: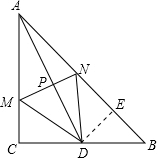 解:如图,设AD与MN交于点P,作DE⊥AB于E.
解:如图,设AD与MN交于点P,作DE⊥AB于E.
∵△ABC是等腰直角三角形,∠C=90°,AC=BC=2,
∴AB=2
.
∵把点A沿MN折叠,点A恰好与BC边的中点D重合,
∴MN垂直平分AD,△AMN≌△DMN,CD=BD=1.
在Rt△ACD中,∵∠C=90°,AC=2,CD=1,
∴AD=
=
,
∴AP=DP=
.
在△APM与△ACD中,
,
∴△APM∽△ACD,
∴
=
,即
=
,
解得PM=
.
在Rt△BED中,∵∠BED=90°,∠B=45°,
∴△BED为等腰直角三角形,
∴BE=DE=
BD=
,
∴AE=AB-BE=2
-
=
.
在△APN与△AED中,
,
∴△APN∽△AED,
∴
=
,即
=
,
解得PN=
,
∴MN=PM+PN=
+
=
,
∴△MND的面积=
MN•DP=
×
×
=
.
故答案为
.
 解:如图,设AD与MN交于点P,作DE⊥AB于E.
解:如图,设AD与MN交于点P,作DE⊥AB于E.∵△ABC是等腰直角三角形,∠C=90°,AC=BC=2,
∴AB=2
| 2 |
∵把点A沿MN折叠,点A恰好与BC边的中点D重合,
∴MN垂直平分AD,△AMN≌△DMN,CD=BD=1.
在Rt△ACD中,∵∠C=90°,AC=2,CD=1,
∴AD=
| AC2+CD2 |
| 5 |
∴AP=DP=
| ||
| 2 |
在△APM与△ACD中,
|
∴△APM∽△ACD,
∴
| PM |
| CD |
| AP |
| AC |
| PM |
| 1 |
| ||||
| 2 |
解得PM=
| ||
| 4 |
在Rt△BED中,∵∠BED=90°,∠B=45°,
∴△BED为等腰直角三角形,
∴BE=DE=
| ||
| 2 |
| ||
| 2 |
∴AE=AB-BE=2
| 2 |
| ||
| 2 |
3
| ||
| 2 |
在△APN与△AED中,
|
∴△APN∽△AED,
∴
| PN |
| ED |
| AP |
| AE |
| PN | ||||
|
| ||||
|
解得PN=
| ||
| 6 |
∴MN=PM+PN=
| ||
| 4 |
| ||
| 6 |
5
| ||
| 12 |
∴△MND的面积=
| 1 |
| 2 |
| 1 |
| 2 |
5
| ||
| 12 |
| ||
| 2 |
| 25 |
| 48 |
故答案为
| 25 |
| 48 |
点评:本题考查了折叠的性质,勾股定理,相似三角形、等腰直角三角形的判定与性质,三角形的面积,综合性较强,有一定难度.准确作出辅助线,求出PM与PN的长是解题的关键.

练习册系列答案
相关题目
若a=5+
,b=3+
,c=1+
,则a、b、c的大小关系是( )
| 15 |
| 17 |
| 19 |
| A、c<b<a |
| B、b<c<a |
| C、c<a<b |
| D、b<a<c |
下列图形中是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 要建一个面积为150m2的长方形养鸡场,为了节约材料,鸡场的一边靠着原有的一条墙,墙长为16m,另三边用竹篱笆围成,已知篱笆总长为35m.则鸡场的宽AB长为
要建一个面积为150m2的长方形养鸡场,为了节约材料,鸡场的一边靠着原有的一条墙,墙长为16m,另三边用竹篱笆围成,已知篱笆总长为35m.则鸡场的宽AB长为 如图,将一根绳子对折以后用线段AB表示,现从P处将绳子剪断,剪断后的各段绳子中最长的一段为12cm,若AP=
如图,将一根绳子对折以后用线段AB表示,现从P处将绳子剪断,剪断后的各段绳子中最长的一段为12cm,若AP= 如图,∠ACB=90°,AC=BC,BE⊥CE于D,AD⊥CE于E,若AD-BE=5cm,则ED=
如图,∠ACB=90°,AC=BC,BE⊥CE于D,AD⊥CE于E,若AD-BE=5cm,则ED= 如图,AB∥ED,∠ECF=70°,则∠BAF的度数为
如图,AB∥ED,∠ECF=70°,则∠BAF的度数为