题目内容
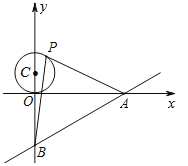
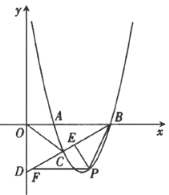
【题目】如图,抛物线![]() 与x轴交于A,B两点,抛物线上另有一点 C在x轴下方,且使ΔOCA∽ΔOBC.
与x轴交于A,B两点,抛物线上另有一点 C在x轴下方,且使ΔOCA∽ΔOBC.
(1)求线段OC的长度;
(2)设直线BC与y轴交于点D,点C是BD的中点时,求直线BD和抛物线的解析式,
(3)在(2)的条件下,点P是直线BC下方抛物线上的一点,过P作![]() 于点E,作PF//AB交BD于点F,是否存在一点P,使得
于点E,作PF//AB交BD于点F,是否存在一点P,使得![]() 最大,若存在,请求出该最大值;若不存在,请说明理由.
最大,若存在,请求出该最大值;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)存在,
;(3)存在,![]() .
.
【解析】
(1)由抛物线![]() 与x轴交于A,B两点,得OA=1,OB=3,由ΔOCA∽ΔOBC.,得
与x轴交于A,B两点,得OA=1,OB=3,由ΔOCA∽ΔOBC.,得![]() ,进而得到答案;
,进而得到答案;
(2)由点C是BD的中点,OC=![]() ,得:a=
,得:a=![]() ,点C的坐标是:(
,点C的坐标是:(![]() ,
,![]() ),再根据待定系数法,求出直线BD和抛物线的的解析式;
),再根据待定系数法,求出直线BD和抛物线的的解析式;
(3)由直线BD的解析式为:![]() ,得:∠OBD=30°,由
,得:∠OBD=30°,由![]() ,PF//AB,得PE=
,PF//AB,得PE=![]() PF,
PF,![]() ,设P坐标为(m,
,设P坐标为(m,![]() ),(
),(![]() ),
),
点F的坐标为(![]() ,
,![]() ),求出PF关于m的函数解析式,即可求出
),求出PF关于m的函数解析式,即可求出![]() 的最大值.
的最大值.
(1)∵抛物线![]() 与x轴交于A,B两点,
与x轴交于A,B两点,
∴A(1,0),B(3,0),即:OA=1,OB=3,
∵ΔOCA∽ΔOBC.,
∴![]() ,即:
,即:![]() ,
,
∴OC=![]() ;
;
(2)∵点C是BD的中点,
∴点C的坐标(![]() ,
,![]() ),
),
∵OC=![]() ,
,
∴![]() ,解得:a=
,解得:a=![]() 或a=-
或a=-![]() (舍去)
(舍去)
∴抛物线的解析式为:![]() ,
,
即:![]()
∴点C的坐标是:(![]() ,
,![]() ),
),
设直线BD的解析式为:y=kx+b,
把(![]() ,
,![]() ),(3,0)代入y=kx+b,
),(3,0)代入y=kx+b,
得: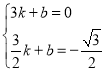 ,解得:
,解得: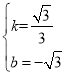 ,
,
∴直线BD的解析式为:![]() ;
;
(3)存在,理由如下:
∵直线BD的解析式为:![]() ,
,
∴点D坐标为(0,![]() ),即:OD=
),即:OD=![]() ,
,
∴tan∠OBD=![]() ,
,
∴∠OBD=30°,
∵![]() ,PF//AB,
,PF//AB,
∴∠PFE=∠OBD=30°,
∴PE=![]() PF,
PF,
∴![]() ,
,
设P坐标为(m,![]() ),(
),(![]() ),
),
则点F的坐标为(![]() ,
,![]() ),
),
∴PF=m-(![]() )=
)=![]() =
=![]() ,
,
∴当m=![]() 时,PF的最大值=
时,PF的最大值=![]() ,此时,
,此时,![]() 的最大值=
的最大值=![]() .
.