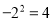题目内容
若关于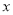 的一元二次方程的两个根为
的一元二次方程的两个根为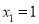 ,
, 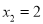 ,则这个方程是( )
,则这个方程是( )
A. 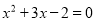 B.
B. 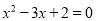 C.
C. 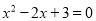 D.
D. 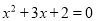
 天天向上口算本系列答案
天天向上口算本系列答案△ABC在平面直角坐标系中的位置如图所示.A(2,3),B(3,1),C(﹣2,﹣2)三点在格点上.
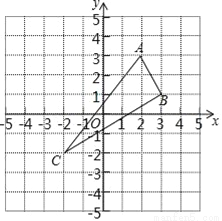
(1)作出△ABC关于y轴对称的△A1B1C1;
(2)直接写出△ABC关于x轴对称的△A2B2C2的各点坐标;
(3)求出△ABC的面积.
(1)作图见解析;(2)A2(2,﹣3),B2(3,﹣1),C2(﹣2,2);(3)6.5. 【解析】试题分析:(1)先得到△ABC关于y轴对称的对应点,再顺次连接即可; (2)先得到△ABC关于x轴对称的对应点,再顺次连接,并且写出△ABC关于x轴对称的△A2B2C2的各点坐标即可; (3)利用轴对称图形的性质可得利用矩形的面积减去三个顶点上三角形的面积即可. 试题解析:...先化简,再求值: 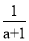 ﹣
﹣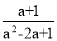 ÷
÷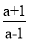 ,其中a=
,其中a=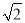 .
.
(1)计算4(x+1)2﹣(2x﹣5)(2x+5).
(2)解方程: 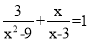 .
.
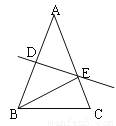
如图,△ABC中,AB=AC=13cm,AB的垂直平分线交AB于D,交AC于E,若△EBC的周长为21cm,则BC= cm.
对于任意不相等的两个实数a、b,定义运算“*”,如下: 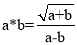 ,如
,如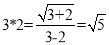 ,那么8*12=_______.
,那么8*12=_______.
若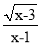 在实数范围内有意义,则x的取值范围是_________
在实数范围内有意义,则x的取值范围是_________
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
甲、乙两班学生参加植树造林,已知甲班每天比乙班多植5棵树,甲班植80棵树所用的天数与乙班植70棵树所用的天数相等,若设甲班每天植树x棵,则根据题意列出的方程是( )
A. 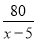 =
=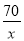 B.
B. 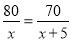 C.
C. 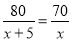 D.
D. 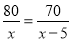
如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE,下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE,其中正确的有( )
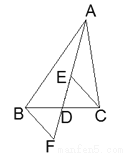
A. 1个 B. 2个 C. 3个 D. 4个
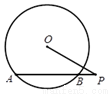
查看答案在数轴上实数a,b的位置如上图所示,化简|a+b|+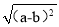 的结果是( )
的结果是( )
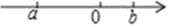
A. ﹣2a﹣b B. ﹣2a+b C. ﹣2b D. ﹣2a
查看答案若分式方程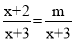 无解,则m的值为( )
无解,则m的值为( )
A. ﹣1 B. 0 C. 1 D. 3
查看答案已知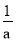 ﹣
﹣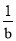 =
=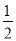 ,则
,则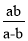 的值为( )
的值为( )
A. 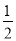 B.
B. 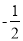 C. ﹣2 D. 2
C. ﹣2 D. 2
如图,AB=AD,要说明△ABC≌△ADE,需添加的条件不能是( )
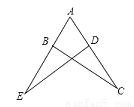
A. ∠E=∠C B. AC=AE C. ∠ADE=∠ABC D. DE=BC
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
计算
①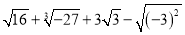
②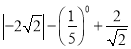
③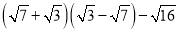
④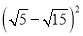
⑤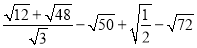
⑥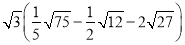
一个直角三角形的斜边长比一直角边长大2,另一直角边长为6,则直角三角形的斜边长为____
查看答案将点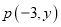 向下平移3个单位长度,向左平移2个单位长度后得到点Q(x,-1),则
向下平移3个单位长度,向左平移2个单位长度后得到点Q(x,-1),则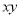 =__________.
=__________.
若已知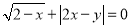 ,那么
,那么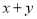 的值为 ___________
的值为 ___________
若一个正数的平方根是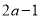 和
和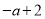 ,则
,则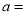 _______,这个正数是___
_______,这个正数是___
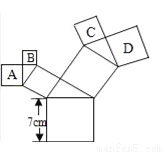
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为______cm2.
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
一元二次方程x(x-3)=4的解是( )
A. 1 B. 4 C. -1或4 D. 1或-4
C 【解析】试题解析:∵x(x-3)=4, ∴x2-3x-4=0, ∴(x-4)(x+1)=0, ∴x-4=0或x+1=0, ∴x1=4,x2=-1. 故选C.已知:点P是∠MAN的角平分线上一点,PB⊥AM于B,PC⊥AN于C.
(1)如图1,点D、E分别在线段AB、AC上,且∠DPE=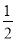 ∠BPC,求证:DE=BD+CE;
∠BPC,求证:DE=BD+CE;
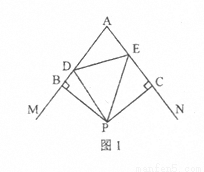
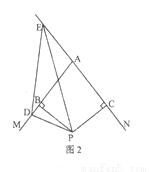
(2)如图2,若D在AB的延长线上,E在直线AC上,则DE、BD、CE三者的数量关系变化吗?若变化,请直接写出结论即可。
阅读下列材料:
(1)解方程: 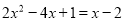
【解析】
方程化为: 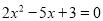 .
.
即化为:(2x-3)(x-1)=0,
∴ 2x-3=0或x-1=0,
解得:x=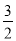 或x=1.
或x=1.
∴方程的根为: 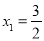 ,
, 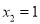 .
.
(2)求解分式方程的过程是:将分式方程化为整式方程,然后求解整式方程,然后将整工方程的根代入验根,舍去增根,得到的根就是原方程的根.
参考上述材料,解决下列问题:
(1)解方程: 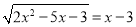 ;
;
(2)若方程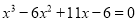 的一个解是x=1,则方程的其他解是__________.
的一个解是x=1,则方程的其他解是__________.
已知:如图,Rt△ABC中,∠BAC=90°.
(1)按要求作图:(保留作图痕迹)
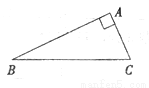
①延长BC到点D,使CD=BC;
②延长CA到点E,使AE=2CA;
③连接AD,BE并猜想线段AD与BE的大小关系;
(2)证明(1)中你对线段AD与BE大小关系的猜想.
【解析】
(1)AD与BE的大小关系是________________.
(2)证明:
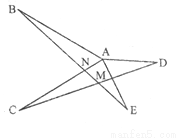
查看答案已知:如图,AB=AC,AD=AE,∠BAC=∠DAE=α,BE与AC、CD分别相交于点N、M.
(1)求证:BE=CD;
(2)求∠BMC的大小.(用α表示)
2017年9月17日,金秋的北京,我校初二全体同学到距学校30千米的房山农业职业学院,参加为期一周的学农劳动。同学们乘坐大巴车前往,李老师因学校有事晚出发了5分钟,开私家车前往,结果和同学们同时到达了农职院。已知李老师开的私家车的速度是大巴车速度的1.2倍,求大巴车和李老师开的私家车的速度分别是多少?
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧


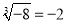 b.
b. 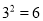 C.
C. 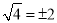 D.
D.