题目内容
7. 如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,点M为边AB上的一动点,点N为边AC上的一动点,且∠MDN=90°,则cos∠DMN为( )
如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,点M为边AB上的一动点,点N为边AC上的一动点,且∠MDN=90°,则cos∠DMN为( )| A. | $\frac{\sqrt{10}}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 连结AD,如图,先利用勾股定理计算出BC=10,再根据直角三角形斜边上的中线性质得DA=DC=5,则∠1=∠C,接着根据圆周角定理得到点A、D在以MN为直径的圆上,所以∠1=∠DMN,则∠C=∠DMN,然后在Rt△ABC中利用余弦定义求∠C的余弦值即可得到cos∠DMN.
解答 解:连结AD,如图,
∵∠A=90°,AB=6,AC=8,
∴BC=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵点D为边BC的中点,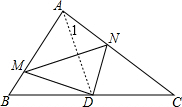
∴DA=DC=5,
∴∠1=∠C,
∵∠MDN=90°,∠A=90°,
∴点A、D在以MN为直径的圆上,
∴∠1=∠DMN,
∴∠C=∠DMN,
在Rt△ABC中,cosC=$\frac{AC}{BC}$=$\frac{8}{10}$=$\frac{4}{5}$,
∴cos∠DMN=$\frac{4}{5}$.
故选D.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.也考查了直角三角形斜边上的中线性质.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
18.己知关于x的不等式组$\left\{\begin{array}{l}{x-a≥1}\\{\frac{2x+1}{5}+1>x}\end{array}\right.$恰有三个整数解,则实数a的取值范围是( )
| A. | -3<a<-2 | B. | -3≤a<-2 | C. | -3<a≤-2 | D. | -3≤a≤-2 |
19. 一个树形图的生长过程如图所示:一个实心圆点到了下一行生成一个空心圆点,一个空心圆到了下以行生成一个实心圆点和一个空心圆点.在某一行中,记空心圆点的数目为m,实心圆点的数目为n,则下列计数不对的是( )
一个树形图的生长过程如图所示:一个实心圆点到了下一行生成一个空心圆点,一个空心圆到了下以行生成一个实心圆点和一个空心圆点.在某一行中,记空心圆点的数目为m,实心圆点的数目为n,则下列计数不对的是( )
 一个树形图的生长过程如图所示:一个实心圆点到了下一行生成一个空心圆点,一个空心圆到了下以行生成一个实心圆点和一个空心圆点.在某一行中,记空心圆点的数目为m,实心圆点的数目为n,则下列计数不对的是( )
一个树形图的生长过程如图所示:一个实心圆点到了下一行生成一个空心圆点,一个空心圆到了下以行生成一个实心圆点和一个空心圆点.在某一行中,记空心圆点的数目为m,实心圆点的数目为n,则下列计数不对的是( )| A. | m=5,n=3 | B. | m=13,n=8 | C. | m=22,n=13 | D. | m=55,n=34 |
16.已知A(2x+1,x-2)关于x轴对称点A′在第二象限,则x的取值范围( )
| A. | x<-$\frac{1}{2}$ | B. | x<2 | C. | x>-$\frac{1}{2}$ | D. | x>2 |
17.把一个周角七等分,求每一份是多少?下列用四舍五入法取近似值正确的是( )
| A. | 50°25′48″(精确到分) | B. | 51°26′(精确到分) | ||
| C. | 51.42°(精确到0.01°) | D. | 51.4°(精确到0.01°) |
 如图,已知一个三角形纸片ABC,BC=10,BC边上的高为8,M为AB边上一动点(点M与点A、B不重合),过点M作MN∥BC,交AC于点,NQ⊥BC,MP⊥BC,垂足分别为Q、P,设MN=x,矩形MNQP的面积为y.
如图,已知一个三角形纸片ABC,BC=10,BC边上的高为8,M为AB边上一动点(点M与点A、B不重合),过点M作MN∥BC,交AC于点,NQ⊥BC,MP⊥BC,垂足分别为Q、P,设MN=x,矩形MNQP的面积为y. 如图,O是半径为R的正六边形的中心.
如图,O是半径为R的正六边形的中心.