题目内容
16. 如图,已知一个三角形纸片ABC,BC=10,BC边上的高为8,M为AB边上一动点(点M与点A、B不重合),过点M作MN∥BC,交AC于点,NQ⊥BC,MP⊥BC,垂足分别为Q、P,设MN=x,矩形MNQP的面积为y.
如图,已知一个三角形纸片ABC,BC=10,BC边上的高为8,M为AB边上一动点(点M与点A、B不重合),过点M作MN∥BC,交AC于点,NQ⊥BC,MP⊥BC,垂足分别为Q、P,设MN=x,矩形MNQP的面积为y.(1)请用x表示MP;
(2)填空:当x=$\frac{40}{9}$时,四边形MNQP是正方形;
(3)求y关于x的函数关系式,并求函数y的最大值.
分析 (1)作AD⊥BC于D,交MN于E,由平行线得出△AMN∽△ABC,由平行线的性质得出$\frac{MN}{BC}=\frac{AE}{AD}$,即可得出结果;
(2)当MN=MP,得出x=-$\frac{4}{5}$x+8,解方程即可;
(3)由矩形的面积得出y=x(-$\frac{4}{5}$x+8)=-$\frac{4}{5}$(x-5)2+20,由-$\frac{4}{5}$<0,得出当x=5时,y有最大值=20即可.
解答 解:(1)作AD⊥BC于D,交MN于E,
∵四边形MNQP是矩形,
∴MP=ED,
∵MN∥BC,
∴△AMN∽△ABC,
∴$\frac{MN}{BC}=\frac{AE}{AD}$,
即$\frac{x}{10}=\frac{8-MP}{8}$,
解得:MP=-$\frac{4}{5}$x+8;
(2)当MN=MP,四边形MNQP是正方形;
即x=-$\frac{4}{5}$x+8,
解得:x=$\frac{40}{9}$,
即当x=$\frac{40}{9}$时,四边形MNQP是正方形;
故答案为:$\frac{40}{9}$;
(3)根据题意得:y=x(-$\frac{4}{5}$x+8)=-$\frac{4}{5}$x2+8x=-$\frac{4}{5}$(x-5)2+20,
∵-$\frac{4}{5}$<0,
∴当x=5时,y有最大值=20.
点评 本题考查了相似三角形的判定与性质、正方形的判定、二次函数的最值;熟练掌握相似三角形的判定与性质,由相似三角形的性质得出MP是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.若a-b=0,且ab≠0,则$\frac{a+b}{b}$的值等于( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
7. 如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,点M为边AB上的一动点,点N为边AC上的一动点,且∠MDN=90°,则cos∠DMN为( )
如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,点M为边AB上的一动点,点N为边AC上的一动点,且∠MDN=90°,则cos∠DMN为( )
 如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,点M为边AB上的一动点,点N为边AC上的一动点,且∠MDN=90°,则cos∠DMN为( )
如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,点M为边AB上的一动点,点N为边AC上的一动点,且∠MDN=90°,则cos∠DMN为( )| A. | $\frac{\sqrt{10}}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
4.为加速南充森林建设,市政府决定对树苗育苗基地实行政府补贴,规定每年培植一亩树苗一次性补贴若干元,随着补贴数字的不断增大,某地苗圃每年育苗规模也不断增加,但每年每亩苗圃的收益会相应下降,经调查每年培植亩数y(亩)与政府每亩补贴数额x(元)之间有如下关系(政府补贴为100元的整数倍,且每亩补贴不超过1000元):
而每年每亩的收益p(元)与政府每亩补贴数额x(元)之间满足一次函数关系p=-5x+9000
(1)请观察题中的表格,用学过的一次函数、反比例函数或二次函数的有关知识求出育苗亩数y(亩)与政府每亩补贴数额x(元)之间的函数关系式;
(2)当2012年政府每亩补贴数额x(元)是多少元时,该地区苗圃收益w(元)最大,最大收益是多少元?
(3)在2012年苗圃取得最大收益的育苗情况下,该地区培植面积刚好达到最大化,要想增收,只能提高每亩收益.经市场调查,培育银杏树苗畅销,每亩的经济效益相应会更好.2013年该地区用去年育苗面积的(30-a)%的土地培育银杏树苗,其余面积继续培植一般类树苗,预计今年培育银杏类树苗每亩收益在去年培植一般类树苗每亩收益的基础上增加了(100+3a)%,由于培育银杏类树苗每亩多支出1000元,2013年该地区因培育银杏类树苗预计比去年增收399万元.请参考以下数据,通过计算,估算出a的整数值.(参考数据:$\sqrt{35}$=5.916,$\sqrt{37}$=6.082,$\sqrt{39}$=6.244)
| x(元) | 0 | 100 | 200 | 300 | 400 |
| y(亩) | 600 | 1000 | 1400 | 1800 | 2200 |
(1)请观察题中的表格,用学过的一次函数、反比例函数或二次函数的有关知识求出育苗亩数y(亩)与政府每亩补贴数额x(元)之间的函数关系式;
(2)当2012年政府每亩补贴数额x(元)是多少元时,该地区苗圃收益w(元)最大,最大收益是多少元?
(3)在2012年苗圃取得最大收益的育苗情况下,该地区培植面积刚好达到最大化,要想增收,只能提高每亩收益.经市场调查,培育银杏树苗畅销,每亩的经济效益相应会更好.2013年该地区用去年育苗面积的(30-a)%的土地培育银杏树苗,其余面积继续培植一般类树苗,预计今年培育银杏类树苗每亩收益在去年培植一般类树苗每亩收益的基础上增加了(100+3a)%,由于培育银杏类树苗每亩多支出1000元,2013年该地区因培育银杏类树苗预计比去年增收399万元.请参考以下数据,通过计算,估算出a的整数值.(参考数据:$\sqrt{35}$=5.916,$\sqrt{37}$=6.082,$\sqrt{39}$=6.244)
 如图,在四边形ABCD中,AD∥BC,AC、DB相交于点O,且∠1=∠2,AB=BC,求证:四边形ABCD是菱形.
如图,在四边形ABCD中,AD∥BC,AC、DB相交于点O,且∠1=∠2,AB=BC,求证:四边形ABCD是菱形. 如图,在△ABC中,AD是角平分线,DE∥AC且交AB于点E,EF∥BC且交AC于点F,求证:AE=CF.
如图,在△ABC中,AD是角平分线,DE∥AC且交AB于点E,EF∥BC且交AC于点F,求证:AE=CF.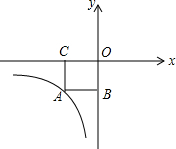 如图,正方形ABOC的边长是2,反比例函数y=$\frac{k}{x}$(x≠0)图象经过点A,则k的值是( )
如图,正方形ABOC的边长是2,反比例函数y=$\frac{k}{x}$(x≠0)图象经过点A,则k的值是( )