题目内容
18.2014年3月27日,湖北省宜昌县发生4.3级地震某校学生全校2000名学生发起了“心系宜昌”捐款活动,为了解捐款情况,学生会随机调查了部分学生捐款情况,并用得到的数据绘制了如图①和图②,根据相关信息解答系列问题:
(1)本次接受随机抽样调查的学生人数为50人,图①中的值是32.
(2)求本次调查获取的样本数据的平均数为16,众数为10,中位数为15;
(3)根据样本数据,估计该校本次活动捐款金额为10元以上(不包含10元)的学生人数.
分析 (1)利用条形统计图得各组的频数,然后把它们相加即可得到抽样调查的学生的总数,再用16除以50即可得到m的值;
(2)根据平均数、众数和中位数的定义求解;
(3)根据样本估计总体,用样本中捐款10元以上所占的百分比表示全校捐款10元以上的百分比,然后计算即可.
解答 解:(1)本次接受随机抽样调查的学生人数为 4+16+12+10+8=50(人),
m%=$\frac{16}{50}$×100%=32%;
故答案为50;32;
(2)本次调查获取的样本数据的平均数为$\frac{4×5+16×10+15×12+10×20+8×30}{50}$=16(元),众数是10元;中位数是15元,
故答案为:16、10、15;
(3)2000×(24%+20%+16%)=1200(人),
答:估计该校捐款10元以上的学生人数有1200人.
点评 本题考查了条形统计图:条形统计图是用线段长度表示数据,根据数量的多少画成长短不同的矩形直条,然后按顺序把这些直条排列起来.从条形图可以很容易看出数据的大小,便于比较.也考查了用样本估计总体、中位数和众数.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
9.已知a+b=4,c-d=-3,则(b-c)-(-d-a)的值为( )
| A. | 7 | B. | -7 | C. | 1 | D. | -1 |
3.二元一次方程组$\left\{\begin{array}{l}{x-y=4}\\{x+y=2}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=3}\\{y=-7}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=7}\\{y=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$ |
10.某校九年级学生从学校去博物馆看展览,学校距离博物馆10千米,一部分同学骑自行车先走,过了20分钟后,其余同学乘汽车出发,结果他们同时到达,已知汽车的速度是骑自行车同学速度的2倍,求骑自行车同学的速度.
(1)设骑车同学的速度为x千米/时,利用速度、时间、路程之间的关系填写下表(要求:填上适当的代数式,完成表格)
(2)列出方程,并求出问题的解.
(1)设骑车同学的速度为x千米/时,利用速度、时间、路程之间的关系填写下表(要求:填上适当的代数式,完成表格)
| 速度(千米/时) | 所用时间(时) | 所走路程(千米) | |
| 骑自行车 | x | $\frac{10}{x}$ | 10 |
| 乘汽车 | 2x | $\frac{10}{2x}$ | 10 |
7. 为增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
为增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
(1)若某用户3月份用气量为60m3,交费多少元?
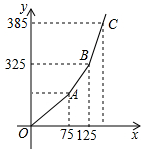
(2)调价后每月支付燃气费用y(单位:元)与每月用气量x(单位:m3)的关系如图所示,求y与x的解析式及a的值.
 为增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
为增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:| 每月用气量 | 单价(元/m3) |
| 不超出75m3的部分 | 2.5 |
| 超出75m3不超过125m3的部分 | a |
| 超出125m3的部分 | a+0.25 |
(2)调价后每月支付燃气费用y(单位:元)与每月用气量x(单位:m3)的关系如图所示,求y与x的解析式及a的值.
 立方体盒子的每个面上都写了一个字,其平面展开图如图所示,那么该立方体盒子上,“强”相对的面上所写的文字是( )
立方体盒子的每个面上都写了一个字,其平面展开图如图所示,那么该立方体盒子上,“强”相对的面上所写的文字是( )