题目内容
已知：如图，在平行四边形ABCD中，点E，F在对角线AC上，且AF=CE．（1）线段BE与DF之间有什么关系？请证明你的结论．
（2）若去掉题设中的AF=CE，请添加一个条件使BE与DF有以上同样的性质．
考点：平行四边形的性质,全等三角形的判定与性质
专题：
分析：（1）利用SAS证明△ADF≌△CBE，从而得出DF与BE平行且相等；
（2）只要添加一个条件，能使得△ADF≌△CBE即可．
（2）只要添加一个条件，能使得△ADF≌△CBE即可．
解答：解：（1）∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠DAF=∠BCE，
在△ADF和△CBE中，
，
∴△ADF≌△CBE（SAS），
∴DF=BE，∠AFD=∠CEB，
∴∠DFC=∠BEA，
∴DF∥BE，
综上可得DF与BE平行且相等；
（2）添加∠CBE=∠ADF．
∴AD∥BC，
∴∠DAF=∠BCE，
在△ADF和△CBE中，
|
∴△ADF≌△CBE（SAS），
∴DF=BE，∠AFD=∠CEB，
∴∠DFC=∠BEA，
∴DF∥BE，
综上可得DF与BE平行且相等；
（2）添加∠CBE=∠ADF．
点评：本题考查了平行四边形的性质，解答本题的关键是证明△ADF≌△CBE，难度一般．
练习册系列答案
相关题目
如图是小兵一天上学、放学时看到的一根电线杆的影子的俯视图，将它们按时间先后顺序进行排列，排列正确的是（ ）
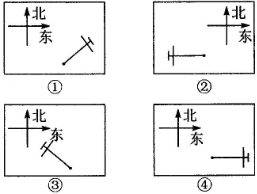
| A、①②③④ | B、②③④① |
| C、②③①④ | D、③①④② |
如图的5个英文字母中，是轴对称图形的有（ ）
| A、2个 | B、3个 | C、4个 | D、5个 |
有下列图形：①线段；②角；③三角形；④等边三角形；⑤平行四边形．其中是中心对称图形的有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
作图题：已知点A，B，C为三个村庄的位置（如图），三村联合打一口井，向三个村庄供水，使水井到三个村庄的距离相等，水井的位置应设在何处？请用尺规画出水井位置，不写作法，保留痕迹．
图中的四个小三角形都是等边三角形，边长为2cm，能通过平移△ABC得到其他三角形吗？若能，请画出平移的方向，并说出平移的距离．