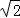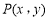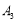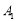题目内容
已知关于
的方程
.
（1）求证：方程总有两个实数根；
（2）若方程的两个实数根都是整数，求正整数
的值.
（1）证明见解析
（2）m=1或2
【解析】
试题分析：（1）要看根的判别式与0的关系，如果大于0，则方程有两个不相等的实数根，如果等于0，则方程有两个相等的实数根，如果小于0，则方程无实数根
（2）利用因式分解法求出方程的两个根，根据方程的根都是实数这一条件去确定正整数m人值
试题解析：
（1）∵
∴原方程总有两个实数根
（2）【解析】
即(x-1)(mx-2)=0
∴x1=1 , x2=
x1=1为整数
∴ x2=为整数即可
所以m=1或2
考点：1、根的判别式；2、因式分解解一元二次方程
练习册系列答案
相关题目
