Question

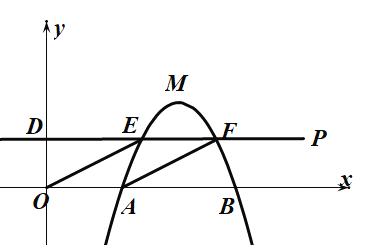
【题目】如图1，抛物线与轴交于点，与轴交于点．

（1）求抛物线的表达式；

（2）点为抛物线的顶点，在轴上是否存在点，使？若存在，求出点的坐标；若不存在，说明理由；

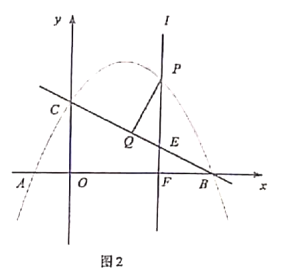
（3）如图2，位于轴右侧且垂直于轴的动直线沿轴正方向从运动到(不含点和点)，分别与抛物线、直线以及轴交于点，过点作于点，求面积的最大值．

Answer 1

【答案】（1）；（2）不存在，理由见解析；（3）最大值为．

【解析】

(1)利用待定系数法求出解析式；

(2) 设点N的坐标为(0，m)，过点M做MH⊥y轴于点H，证得△MHN∽△NOB，利用对应边成比例，得到，方程无实数解，所以假设错误，不存在；

(3) △PQE∽△BOC，得，得到，当PE最大时，最大，求得直线的解析式，设点P的坐标为 ，则E，再求得PE的最大值，从而求得答案．

(1) 把点A（-2，0）、B（8，0）、C（0，4）分别代入，得：

，

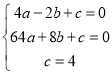解得，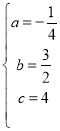

则该抛物线的解析式为：；

(2)不存在

∵抛物线经过A（-2，0）、B（8，0），

∴抛物线的对称轴为，

将代入得：，

∴抛物线的顶点坐标为： ，

假设在轴上存在点，使∠MNB=90，

设点N的坐标为(0，m)，过顶点M做MH⊥y轴于点H，

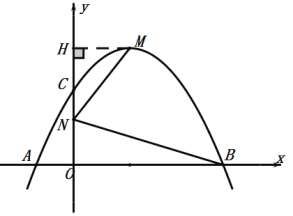
∴∠MNH+∠ONB=90，∠MNH+∠HMN=90，

∴∠HMN=∠ONB，

∴△MHN∽△NOB，

∴，

∵B（8，0），N (0，m)， ，

∴，

∴，

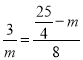整理得：，

∵，

∴方程无实数解，所以假设错误，

在轴上不存在点，使∠MNB=90；

(3) ∵PQ⊥BC，PF⊥OB，

∴，

∴EF∥OC，

∴，

∴△PQE∽△BOC，

得，

∵B（8，0）、C（0，4），

∴，，，

∴，

∴，

∴当PE最大时，最大，

设直线的解析式为，

将B（8，0）、C（0，4）代入得，

解得：，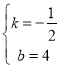

∴直线的解析式为，

设点P的坐标为 ，

则点E的坐标为，

∴，

∵，

∴当时，有最大值为4，

∴最大值为．