Question

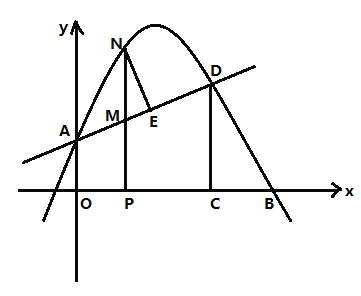
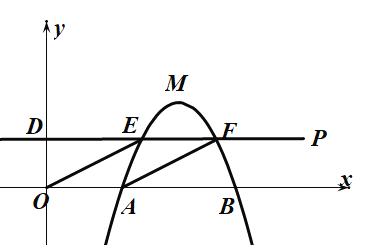
【题目】已知二次函数y＝﹣x2+bx+c的图象经过点A（2，0），B（5，0），过点D（0，）作y轴的垂线DP交图象于E、F．

（1）求b、c的值和抛物线的顶点M的坐标；

（2）求证：四边形OAFE是平行四边形；

（3）将抛物线向左平移的过程中，抛物线的顶点记为M′，直线DP与抛物线的左交点为E′，连接OM′，OE′，当OE′+OM′的值最小时求直线OE′的解析式．

Answer 1

【答案】（1）b＝7，c＝﹣10，M的坐标为（，）；（2）见解析；（3）OE′的解析式为y＝﹣x

【解析】

（1）由抛物线的交点式可直接得到抛物线的解析式，从而可求得b、c的值，然后利用配方法可求得顶点M的坐标；

（2）先求得点E和点F的坐标，从而可得到EF＝OA，然后依据平行四边形的判定定理进行证明即可；

（3）设抛物线向左平移m个单位时，则M′（﹣m，），E′（﹣m，），作点M′关于x轴的对称点M″，则点M″（﹣m，﹣），当点E′、O、M″在一条直线上时，OE′+OM′有最小值，然后再依据E′M″的图象为正比例函数图象列出关于m的比例式，从而可求得m的值，然后可求得OE′的解析式．

解：（1）抛物线解析式为y＝﹣（x﹣2）（x﹣5），即y＝﹣x2+7x﹣10，

∴b＝7，c＝﹣10，

∵y＝﹣x2+7x﹣10＝﹣（x﹣）2+，

∴顶点M的坐标为（，）；

（2）证明：当y＝时，﹣（x﹣）2+＝，

解得x1＝，x2＝，

则E（，），F（，），

∵EF＝﹣＝2，

而OA＝2，

∴EF＝OA，

∵EF∥OA，

∴四边形OAFE是平行四边形；

（3）设抛物线向左平移m个单位时，OE′+OM′有最小值，则M′（﹣m，），E′（﹣m，），作点M′关于x轴的对称点M″，则点M″（﹣m，﹣）．

由轴对称的性质可知：OM′＝OM″，则OE′+OM′＝OE′+OM″．

∴当点E′、O、M″在一条直线上时，OE′+OM′有最小值．

∴，

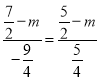解得：m＝．

∴k＝＝﹣．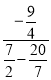

∴OE′的解析式为y＝﹣x．