Question

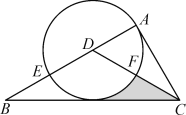
【题目】如图，在△ABC中，AB＝AC＝5，BC＝8，点D是边BC上（不与B，C重合）一动点，∠ADE＝∠B＝a，DE交AC于点E，下列结论：①AD2＝AE．AB；②1.8≤AE＜5；⑤当AD＝时，△ABD≌△DCE；④△DCE为直角三角形，BD为4或6.25．其中正确的结论是_____．（把你认为正确结论序号都填上）

Answer 1

【答案】①②④．

【解析】

①易证△ABD∽△ADF，结论正确；

②由①结论可得：AE=，再确定AD的范围为：3≤AD＜5，即可证明结论正确；

③分两种情况：当BD＜4时，可证明结论正确，当BD＞4时，结论不成立；故③错误；

④△DCE为直角三角形，可分两种情况：∠CDE=90°或∠CED=90°，分别讨论即可．

解：如图，在线段DE上取点F，使AF=AE，连接AF，

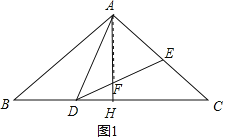
则∠AFE=∠AEF，

∵AB=AC，

∴∠B=∠C，

∵∠ADE=∠B=a，

∴∠C=∠ADE=a，

∵∠AFE=∠DAF+∠ADE，∠AEF=∠C+∠CDE，

∴∠DAF=∠CDE，

∵∠ADE+∠CDE=∠B+∠BAD，

∴∠CDE=∠BAD，

∴∠DAF=∠BAD，

∴△ABD∽△ADF

∴，即AD2=ABAF

∴AD2=ABAE，

故①正确；

由①可知：，

当AD⊥BC时，由勾股定理可得：

，

∴，

∴，即，故②正确；

如图2，作AH⊥BC于H，

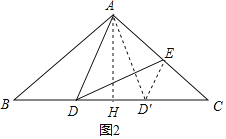
∵AB=AC=5，

∴BH=CH=BC=4，

∴，

∵AD=AD′=，

∴DH=D′H=，

∴BD=3或BD′=5，CD=5或CD′=3，

∵∠B=∠C

∴△ABD≌△DCE（SAS），△ABD′与△D′CE不是全等形

故③不正确；

如图3，AD⊥BC，DE⊥AC，

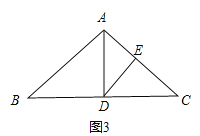
∴∠ADE+∠DAE=∠C+∠DAE=90°，

∴∠ADE=∠C=∠B，

∴BD=4；

如图4，DE⊥BC于D，AH⊥BC于H，

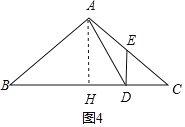
∵∠ADE=∠C，

∴∠ADH=∠CAH，

∴△ADH∽△CA，

∴，即，

∴DH=，

∴BD=BH+DH=4+==6.25，

故④正确；

综上所述，正确的结论为：①②④；

故答案为：①②④.