题目内容
16. 如图,在正方形ABCD中,点E、F在AD的延长线上,DE=DA,DF=DB,H、G分别为BF和DC、CE的交点,求证:GH=GF.
如图,在正方形ABCD中,点E、F在AD的延长线上,DE=DA,DF=DB,H、G分别为BF和DC、CE的交点,求证:GH=GF.
分析 如图,连接BD、DG.只要证明△BCG是底角等于22.5°的等腰三角形,即可推出,BC=CG=CD,推出∠GDH=∠GHD=67.5°,∠GDF=∠F=22.5°,即可解决问题.
解答 证明:如图,连接BD、DG.
∵四边形ABCD是正方形,
∴∠ADB=45°,∠BCD=∠ADC=∠CDE=90°,
∵DE=DC,
∴∠DCE=45°,
∵DB=DF,
∴∠DBF=∠F,
∵∠ADB=∠DBF+∠F=45°,
∴∠DBF=∠F=22.5°,
∴∠BHC=∠DHG=67.5°,∠BCG=135°,
∴∠BGC=180°-135°-22.5°=22.5°,
∴∠CBG=∠CGB,
∴CB=CG=CD,
∴∠CDG=∠CGD=67.5°,
∴∠GDH=∠GHD=67.5°,∠GDF=∠F=22.5°,
∴DG=GH,GF=DG,
∴HG=FG.
点评 本题考查正方形的性质、等腰三角形的性质和判定、等腰直角三角形的性质等知识,解题的关键是通过角度计算,发现等腰三角形,属于中考常考题型.

练习册系列答案
相关题目
6.下列解方程过程中,变形正确的是( )
| A. | 由x+5=6x-7得5x=5-7 | B. | 由-2(x-1)=3得-2x-2=3 | ||
| C. | 由$\frac{x-3}{0.7}$=1得$\frac{10x-30}{7}$=10 | D. | 由$\frac{1}{2}$x+9=-$\frac{3}{2}$x-3得2x=-12 |
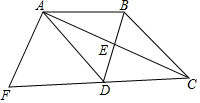 如图,四边形ABCD中,BD垂直平分AC,垂足为点E,点F为四边形ABCD外一点,DA平分∠BDF,∠ADF=∠BAD,且AF⊥AC.
如图,四边形ABCD中,BD垂直平分AC,垂足为点E,点F为四边形ABCD外一点,DA平分∠BDF,∠ADF=∠BAD,且AF⊥AC. 如图,已知?ABCD中,对角线AC与BD交于点O,∠ABD=2∠DBC,AE⊥BD于E.
如图,已知?ABCD中,对角线AC与BD交于点O,∠ABD=2∠DBC,AE⊥BD于E.