题目内容
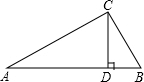 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,AC=6
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,AC=6| 3 |
(1)求∠A的度数;
(2)求BC的长及△ABC的面积.
考点:射影定理
专题:计算题
分析:(1)先利用射影定理得到AC2=AD•AB,即(6
)2=AD•(AD+3),再解方程得到AD=9,然后根据正弦的定义求∠A;
(2)先根据含30度的直角三角形三边的关系求BC,然后根据三角形面积公式求△ABC的面积.
| 3 |
(2)先根据含30度的直角三角形三边的关系求BC,然后根据三角形面积公式求△ABC的面积.
解答:解:(1)∵∠ACB=90°,CD⊥AB于点D,
∴AC2=AD•AB,即(6
)2=AD•(AD+3),
整理得AD2+3AD-108=0,解得AD=9或AD=-12(舍去),
在Rt△ACD中,∵cosA=
=
=
,
∴∠A=30°;
(2)∵AB=AD+BD=9+3=12,
而∠A=30°,
∴BC=
AB=6,
∴S△ABC=
•AC•BC=
•6
•6=18
.
∴AC2=AD•AB,即(6
| 3 |
整理得AD2+3AD-108=0,解得AD=9或AD=-12(舍去),
在Rt△ACD中,∵cosA=
| AD |
| AC |
| 9 | ||
6
|
| ||
| 2 |
∴∠A=30°;
(2)∵AB=AD+BD=9+3=12,
而∠A=30°,
∴BC=
| 1 |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
点评:本题考查了射影定理:直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项;每一条直角边是这条直角边在斜边上的射影和斜边的比例中项.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
如果一个多项式的次数是5,那么这个多项式的任何一项的次数满足( )
| A、都小于5 | B、都大于5 |
| C、都不小于5 | D、都不大于5 |
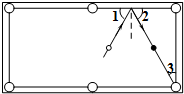 在长方形台球桌上打台球时,球的反射角∠1等于入射角∠2,如图所示.如果∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1的度数为( )
在长方形台球桌上打台球时,球的反射角∠1等于入射角∠2,如图所示.如果∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1的度数为( )| A、30° | B、45° |
| C、60° | D、75° |
 如图,点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点(其中P、Q不与端点重合),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ、CP交于点M,则在P、Q运动的过程中,下列结论:(1)BP=CM;(2)△ABQ≌△CAP;(3)∠CMQ的度数始终等于60°;(4)当第
如图,点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点(其中P、Q不与端点重合),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ、CP交于点M,则在P、Q运动的过程中,下列结论:(1)BP=CM;(2)△ABQ≌△CAP;(3)∠CMQ的度数始终等于60°;(4)当第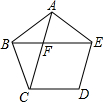 如图,在正五边形ABCDE中,对角线AC,BE相交于点F,F是线段BE、AC的黄金分割线吗?为什么?
如图,在正五边形ABCDE中,对角线AC,BE相交于点F,F是线段BE、AC的黄金分割线吗?为什么?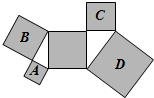 如图,所有阴影部分的四边形都是正方形,所有三角形都是直角三角形,已知正方形A、B、C的面积依次为2、4、3,则正方形D的面积为
如图,所有阴影部分的四边形都是正方形,所有三角形都是直角三角形,已知正方形A、B、C的面积依次为2、4、3,则正方形D的面积为