题目内容
20.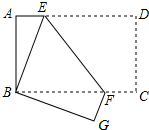 如图,将长方形纸片ABCD折叠,使点D与B重合,点C落到G处,折痕为EF,若∠ABE=20°,则∠EFG的度数为( )
如图,将长方形纸片ABCD折叠,使点D与B重合,点C落到G处,折痕为EF,若∠ABE=20°,则∠EFG的度数为( )| A. | 125° | B. | 120° | C. | 135° | D. | 150° |
分析 由折叠的性质知:∠EBG、∠BGF都是直角,∠BEF=∠DEF,因此BE∥GF,那么∠EFG和∠BEF互补,即可解答.
解答 解:由折叠的性质知,∠BEF=∠DEF,∠EBG=∠D=90°,∠BGF=∠C=90°,
∴BE∥GF,
∴∠EFG+∠BEF=180°,
又∵∠ABE=20°,
∴∠AEB=70°,
∴∠BEF=∠DEF=55°,
∴∠EFG=180°-55°=125°.
故选A.
点评 本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后对应角相等.

练习册系列答案
相关题目
10.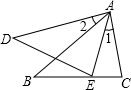 如图,已知∠1=∠2,下列条件①$\frac{AB}{AD}$=$\frac{AC}{AE}$;②$\frac{AB}{AD}$=$\frac{BC}{DE}$;③∠B=∠D;④∠C=∠AED,能判定△ABC∽△ADE的有( )
如图,已知∠1=∠2,下列条件①$\frac{AB}{AD}$=$\frac{AC}{AE}$;②$\frac{AB}{AD}$=$\frac{BC}{DE}$;③∠B=∠D;④∠C=∠AED,能判定△ABC∽△ADE的有( )
 如图,已知∠1=∠2,下列条件①$\frac{AB}{AD}$=$\frac{AC}{AE}$;②$\frac{AB}{AD}$=$\frac{BC}{DE}$;③∠B=∠D;④∠C=∠AED,能判定△ABC∽△ADE的有( )
如图,已知∠1=∠2,下列条件①$\frac{AB}{AD}$=$\frac{AC}{AE}$;②$\frac{AB}{AD}$=$\frac{BC}{DE}$;③∠B=∠D;④∠C=∠AED,能判定△ABC∽△ADE的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.下列计算正确的是( )
| A. | 23=2×3 | B. | -210=(-2)10 | C. | (-2)3=-23 | D. | (2+3)2=22+32 |