题目内容
11.如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.(1)探究猜想:①∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③猜想图1中∠AED、∠EAB、∠EDC的关系并说明理由.
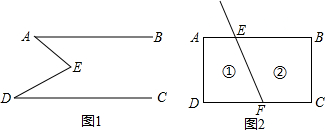
(2)拓展应用,如图2,线段FE与长方形ABCD的边AB交于点E,与边CD 交于点F.图2中①②分别是被线段FE隔开的2个区域(不含边界),P是位于以上两个区域内的一点,猜想∠PEB,∠PFC,∠EPF的关系(不要求说明理由)
分析 (1)①过点E作EF∥AB,再由平行线的性质即可得出结论;
②、③根据①的过程可得出结论;
(2)根据题意画出图形,再根据平行线的性质及三角形内角和定理即可得出结论.
解答 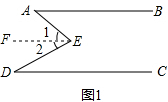 解:(1)①过点E作EF∥AB,
解:(1)①过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∵∠A=30°,∠D=40°,
∴∠1=∠A=30°,∠2=∠D=40°,
∴∠AED=∠1+∠2=70°;
②过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∵∠A=20°,∠D=60°,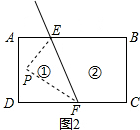
∴∠1=∠A=20°,∠2=∠D=60°,
∴∠AED=∠1+∠2=80°;
③猜想:∠AED=∠EAB+∠EDC.
理由:过点E作EF∥CD,
∵AB∥DC∴EF∥AB(平行于同一条直线的两直线平行),
∴∠1=∠EAB,∠2=∠EDC(两直线平行,内错角相等),
∴∠AED=∠1+∠2=∠EAB+∠EDC(等量代换).
(2)如图2,当点P在①区域时,
∵AB∥CD,
∴∠BEF+∠CFE=180°,
∴∠PEF+∠PFE=(∠PEB+∠PFC)-180°.
∵∠PEF+∠PFE+∠EPF=180°,
∴∠EPF=180°-(∠PEF+∠PFE)=180°-(∠PEB+∠PFC)+180°=3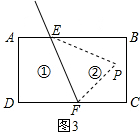 60°-(∠PEB+∠PFC);
60°-(∠PEB+∠PFC);
当点P在区域②时,如图3所示,
∵AB∥CD,
∴∠BEF+∠CFE=180°,
∵∠EPF+∠FEP+∠PFE=180°,
∴∠EPF=∠PEB+∠PFC.
点评 本题考查的是平行线的性质,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
1.在下面四根木棒中,选一根能与长为4cm,9cm的两根木棒首尾依次相接钉成一个三角形的是( )
| A. | 4cm | B. | 5cm | C. | 9cm | D. | 13cm |
3.关于x的一元二次方程(m-1)x2+x+m2-1=0的一个根是0,则m的值为( )
| A. | 1 | B. | 1或-1 | C. | -1 | D. | 0.5 |
1. 如图,直线a,b被直线c所截,a∥b,∠2=∠3,若∠1=80°,则∠4等于( )
如图,直线a,b被直线c所截,a∥b,∠2=∠3,若∠1=80°,则∠4等于( )
 如图,直线a,b被直线c所截,a∥b,∠2=∠3,若∠1=80°,则∠4等于( )
如图,直线a,b被直线c所截,a∥b,∠2=∠3,若∠1=80°,则∠4等于( )| A. | 20° | B. | 40° | C. | 60° | D. | 80° |